事件独立性：概率论与数理统计

事件的独立性,在概率论中具有特殊重要性。

对于试验E 的两个事件A,B,若P(B)＞0,可以定义P(A|B),一般来说B 的发生对A发生的概率有影响,这时P(A|B)≠P(A),只有在影响不存在时才会有P(A|B)=P(A)。

定义1.6.1 如果P(A|B)=P(A)或P(B|A)=P(B),则称A,B 是相互独立的事件或简称事件A,B 独立。

在实际问题中,往往是从直观上判断事件A,B 是否独立,如果事件A 发生与否不影响事件B 发生的概率(反过来,事件B 发生与否不影响事件A 发生的概率),我们说事件A,B 是相互独立的。

若事件A,B 相互独立,由乘法公式知

在理论上,人们用式(1.6.1)作为事件A,B 相互独立的定义。

例1.6.1 设试验E 为“抛掷甲、乙两枚硬币,观察正反面出现的情况”。设事件A 表示“甲币出现H”,事件B 表示“乙币出现H”,E 的样本空间为

所以

有

所以事件A,B 相互独立,实际从试验的直观判断看事件A 发生与否不影响事件B 发生的概率,两者是一致的。

定义1.6.2 3个事件A,B,C 相互独立用下面4个式子来定义

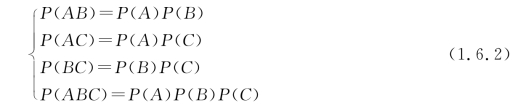
严格从定义上看,前3个式子的成立,只表明A,B,C3个事件两两独立,由于用前三式导不出第四式,故两两独立,不一定相互独立,但相互独立,一定两两独立。

定义1.6.3 n个事件A1,A2,…,An 相互独立是由下列2n-n-1个式子定义的。

如前所述,在实际中,人们往往通过经验或专业知识来判断事件之间是否独立,若独立,则可用式(1.6.2)和式(1.6.3),这给概率的计算带来了很大的方便。

若事件A,B 是相互独立的,容易证明与B,A 与也是相互独立的。

事实上,假设事件A 和B 相互独立,首先证明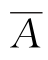和B 也独立。由P(AB)=P(A)P(B),可见

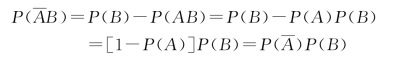
从而A和B 独立。这样,我们证明了:如果两事件独立,则其中一个事件换成其对立事件,所得两个事件仍然独立。因此,由A 和B 独立,可见A 和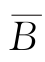 独立;而由A 和 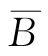独立,可见独立。

若n个事件A1,A2,…,An 相互独立,则将它们之中任意m(1≤m≤n)个事件换成其对立事件后,所得n个事件仍然相互独立,证明同两个事件类似。

例1.6.2 若生产某产品经过5道工序,每道工序的不合格率分别为0.01,0.02,0.03,0.04,0.05,假定工序之间是相互独立的,求该产品的合格率和不合格率。(www.xing528.com)

解 设Ai={第i道工序生产合格},i=1,2,3,4,5,则

例1.6.3 一电路系统由元件A 和2个并联的元件B 与C 串联而成(图1.6.1)。假设3个元件的状态(好与坏)相互独立;元件A,B,C 损坏的概率相应为0.3、0.2、0.2,求该电路系统因元件损坏而不通的概率α。

图1.6.1

解 以A,B 和C 分别表示事件{A 损坏},{B 损坏}和{C 损坏};由条件知事件A,B 和C相互独立。易见,事件“电路因元件损坏而不通”等于A∪BC。因此,由事件A,B 和C 的独立性知,电路因元件损坏而不通的概率为

例1.6.4 设P(A)=0.4,P(A∪B)=0.7,求P(B),已知(1)事件A 和B 互不相容;(2)事件A 和B 相互独立。

解 对于任意事件A 和B,由加法公式,有

得

(1)设事件A 和B 不相容,即AB=∅,则P(AB)=0,因此

(2)设事件A 和B 相互独立,则P(AB)=P(A)P(B),因此

例1.6.5 设某科学工作者每次试验成功的概率是0.01,试问他要做多少次试验才能十拿九稳地做到试验成功(假定试验与试验之间是相互独立的)?

解 设某科学工作者要做N 次试验才能十拿九稳地使试验成功,即N 次试验至少有一次成功的概率是90%,又设F={某科学工作者一次试验失败},C={某科学工作者N 次试验失败},由题设知

两边取对数得到

由此解出

[x]表示不超过x 的最大整数。