贝叶斯公式：概率论与数理统计

设Ω 为试验E 的样本空间,A 为E 的事件,B1,B2,…,Bn 为完备事件组,即满足两两互斥事件,且P(A)＞0,P(Bi)＞0(i=1,2,…,n)则

证明 依式(1.5.1)有P(Bj|A)=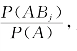又依全概率公式有P(A)=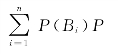代入式(1.5.7)即得证。

例1.5.5 8支枪中,有3支未经试射校正,5支已经试射校正。用校正过的枪射击时,中靶的概率为0.8,用未校正的枪射击时,中靶的概率为0.3,今从8支枪中任取一支射击中靶。问所用这支枪是校正过的概率是多少?

解 设事件A={射击中靶},B1={任取一支枪是校正过的},B2={任取一支枪是未校正过的},B1,B2 构成完备事件组,则

故所求概率为

例1.5.6 某电子设备制造商所用的元件由3家元件制造厂提供,根据以往的记录有以下数据:

设这3家工厂的产品在仓库中是均匀混合的,且无区别的标志。(1)在仓库中随机地取一只元件,求它是次品的概率;(2)在仓库中随机地取一只元件,若已知取到的元件是次品,那么,该元件由3家工厂生产的概率分别是多少? 并根据结果分析该次品元件出自何厂。

解 设A 表示“取到的是一只次品”,Bi(i=1,2,3)表示“所取到的产品是由第i家工厂提供的”。易知,B1,B2,B3 构成样本空间Ω 的一个完备事件组,且有

(1)根据全概率公式,知

(2)由贝叶斯公式,知

以上结果表明,这只次品来自第2家工厂的可能性最大。

例1.5.7 根据美国的一份资料报道,在美国总体来说患肺癌的概率约为0.1%,在人群中有20%是吸烟者,他们患肺癌的概率约为0.4%,求不吸烟者患肺癌的概率是多少?

解 以C 记事件“患肺癌”,以A 记事件“吸烟”,按题意P(C)=0.001,P(A)=0.20,P(C|A)=0.004,不吸烟者患肺癌的概率可用)表示。

由全概率公式知,(www.xing528.com)

将数据代入,得

另一解法:

例1.5.8 根据以往的临床记录,某种诊断癌症试验具有以下效果:若以A 表示事件“试验反应为阳性”,以C 表示事件“被诊断者患癌症”,则有现在对自然人群进行普查,设被试验的人患癌症的概率为0.005,即P(C)=0.005,试求

解 已知由贝叶斯公式,得

结果表明,尽管都很高,但将此用于普查癌症检验为阳性确实患癌症的概率只有,即其正确性只有8.7%(平均1000个具有阳性反应的人中大约只有87人患癌症),如果不注意这点,将会得出错误的诊断,这说明混淆和会造成不良后果。

例1.5.9 商店的玻璃杯成箱出售,每箱20只。假设每箱含0,1,2只残品的概率分别为0.8,0.1和0.1。有一顾客欲买一箱玻璃杯,售货员随意取一箱交给顾客,而顾客只随意察看其中4只,结果未发现残品,于是买下。试求在顾客买下的一箱中确实无残品的概率β。

解 引进事件:A={顾客买下所察看的一箱},Hi={箱中恰有i件残品}(i=0,1,2)。由条件知

由全概率公式,可知

于是,由贝叶斯公式,得

例1.5.10 对以往数据进行分析结果表明,当机器调整得良好时,产品的合格率为98%,而当机器发生某种故障时,其合格率为55%。每天早上机器开动时,机器良好的概率为95%,试求已知早上第一件产品是合格品时,机器调整良好的概率是多少?

解 设A 为事件“产品合格”,B 为事件“机器调整良好”。0.55,P(B)=0.95,所求概率由贝叶斯公式,得

即当第一件产品是合格品时,此时机器调整良好的概率为0.97,这里概率0.95是由以往的经验分析得到的,叫作先验概率,而得到信息(生产第一件产品是合格品)后再重新加以修正的概率(即0.97)叫作后验概率。