为了确定宽频激励源的激励幅值,采用图5.5(a)所示的52个加速度计测得的振速幅值数据,同时在有限元模型中相同位置、方向施加幅值为1N的谐和激励,由于外壳节点数达到了13588,如果采用传统的FE-BE方法,仅边界元矩阵的存储空间就达到了5.6GB,耦合矩阵及其稀疏LU分解因子所需的空间更大,无法在本文的计算环境下实现,因此仅采用上文的K-Schur求解器计算得到相应位置上的振速幅值,其中试验测得均方振速级如图5.16所示,仿真计算得到均方振速级如图5.17所示。
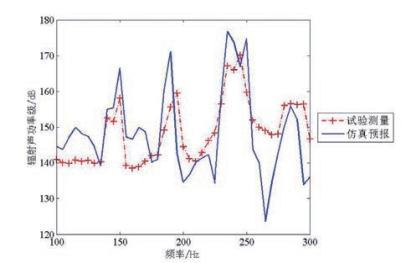
图5.16 试验测量均方振速级(单一中心激励)
Fig5.16 Experimental measurement of mean square velocity level(single center excitation conditions)
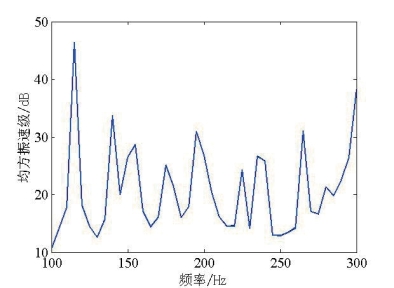
图5.17 仿真计算均方振速级(单一中心激励)
Fig5.17 Simulation calculation of mean square velocity level(single center excitation conditions)
对比图5.16与图5.17可以发现,由于试验所采用激励源的能量分布频带非常宽,使得采用1N单频谐和激励计算得到的均方振速远大于试验中通过宽频脉冲激励测得的均方振速。由于本文只考虑线性范围内的振动与声辐射,因此只需要将仿真计算的声压、位移解根据试验测量结果按比例调整,即可有效的模拟试验中的激励响应。
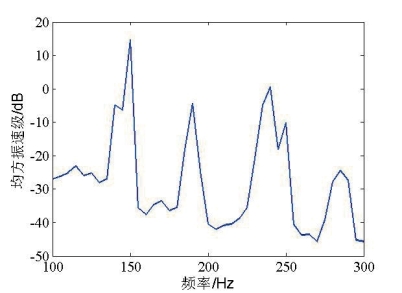
图5.18 辐射声功率对比图(单一中心激励)
Fig5.18 Comparison of radiate sound power level(single center stimulation)
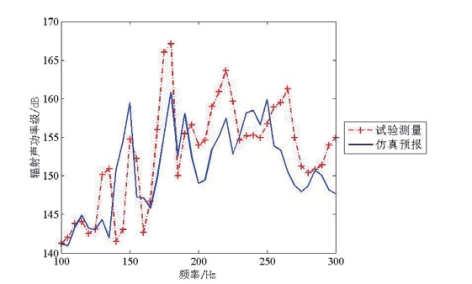
图5.19 辐射声功率对比图(两侧对称激励)
Fig5.19 Comparison of radiate sound power level(bilateral symmetry excitation condition)
由图5.18和5.19可以看出,在100-300Hz频段内,有限元-ACA边界元法数值预报与试验测量辐射声功率具有一致的基本趋势,但仍有较多频点差别较大,尤其是在两侧对称激励工况下,250Hz处峰值出现了明显的偏移,分析原因如下:(https://www.xing528.com)
1)为了方便组装,模型的外壳体实际由多片弧形钢板组成并紧固于肋板上,钢板之间存在细微的缝隙,而数值仿真模型直接将其简化为一个整体,可能引入了额外的低阶模态;
2)试验模型中起支撑作用的肋板为大量离散的扇形结构组成,而本章将其简化为完全支撑的实肋板,也带来了一定的误差。
此外,试验与数值预报结果随频率变化的趋势一致性表明,本文所采用的基于内壳均方振速数据为数值仿真提供修正的方法是可行的,同时也证明本文建立的有限元-ACA边界元法是可靠的。

图5.20 不同激励情况下求解迭代次数
Fig5.20 Iterate numbers of solver under different stimulation
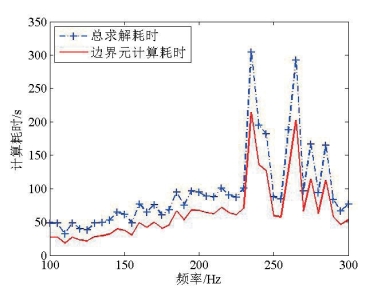
图5.21 中心激励情况下求解耗时
Fig5.21 Time cost of solver under single center stimulation
图5.20给出了两种激励条件下,K-Schur求解器迭代次数随频率变化的曲线,由图中可以看出,两种激励条件下求解器达到收敛速度有很高的一致性,各频点处迭代次数的差别在2次以内;在大部分的求解频率下,求解器均在30次以内获得了收敛,只有在235Hz、245Hz、260Hz、275Hz和285Hz等少数频点上收敛较慢,但未出现不收敛的情况。
如图5.21所示,中心激励条件下求解器的总耗时曲线和边界元计算耗时曲线的趋势一致但幅度不同,求解边界元方程的计算耗时占总计算时间的67.7%,这说明第三章提出的迭代求解器具有较稳定的计算效率,同时也说明通过提高边界元求解器的并行水平还可以较大幅度的改善求解器的求解速度。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




