1.有限元模型的建立
首先采用有限元软件ANSYS建立双层圆柱壳体的有限元模型,对于相对较薄的内、外壳以及隔板,采用ANSYS软件中的SHELL63单元。由于模型两侧端板的厚度较大,采用实体单元对其进行描述。在此基础上对模型进行简化:
1)忽略流水孔的存在,将肋板看作完整的环形面进行处理;
2)忽略端盖,将模型两端的盖板看作完整的圆形面;
3)与模型相比,脉冲激振源的尺寸较小,因此将其近似为附着在内壳内部、大小为50KG的质量负载。
值得注意的是,双层圆柱壳舷间流场可近似看作一个空心圆柱形的区域,在它的内部沿轴向均匀分布着15块较薄的实肋板作为支撑部件,在忽略肋板厚度的情况下,通过将其视为奇异边界,采用双重边界元法或子结构边界元法都可以很容易的求解相应的内场声辐射问题,然而要实现其与有限元法的耦合却要面临两方面困难:
1)流体区域形状扁而长,其体积与面积的比值较小,采用边界元法并不经济;
2)由于肋板与内外壳相连,在环形面的内、外边缘处,网格节点同时处于两个甚至三个流体区域的边界上,而这些流体区域在此处的法线方向并不一致,同时很难保证彼此正交以构成局部坐标系,也就不能实现位移与法向振速之间的正确转换。
基于以上考虑,本节采用无粘性、可压缩流体模型,利用有限元法离散两层壳体之间的流体。设流体声速为c,单元所在区域为Ve,形函数矩阵为N,则声压格式的流体单元刚度、质量矩阵可由式(5-5)导出。
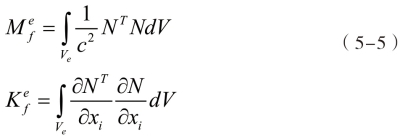
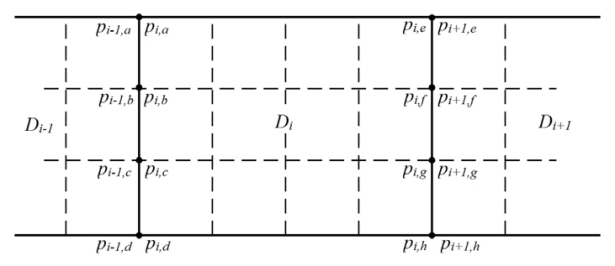
此外由于采用了面单元对肋板进行描述,使得肋板两侧不同的流体子区域之间存在公共节点,而它们之间显然没有声压连续的关系,因此必须在有限元方程中对肋板两侧的声压自由度加以区分,如图5.8所示。
 (https://www.xing528.com)
(https://www.xing528.com)
图5.8 自由度区分示意图
Fig5.8 Division of degree of freedoms
2.网格的划分
足够的网格密度是保证计算精确度的必要条件。振动与声波单元密度过低,虽然计算速度较快,但精度不足;密度过高,精度提高,但相应的计算量,尤其是针对实体结构,频率过高,又必须考虑计算能力。由于本文直接采用结构有限元网格的外表面部分作为声场的边界元网格,因此在划分结构有限元网格时,应同时考虑结构振动分析和声辐射预报分析对网格收敛性的要求。
根据香农采样定理[124],当每个波长内含有两个采样点时,该频率下的波动即可被检测到。然而Schmiechen[125]在研究轴对称结构的模态分析时发现,要准确的还原结构的模态振型,采样点的密度应至少提高三倍,达到每波长六个节点。此外,四分之一波动细化准则[126,127]认为,要对应力波进行较为准确的描述,则每个波长至少需要五个节点,也即四个单元,据此得出单元尺寸D≤(1/4)lmin的网格细化标准,其中lmin为最小应力波长。在经典的梁、板问题中,应力波长随频率的变化可由理论公式明确地给出,但对于双层壳体结构,其应力波的形式较为复杂,很难得出相应的规律。
由于自由场中声波的波长只与介质声速和频率有关,因此声学边界元法的网格收敛性理论相对简单。S.Marburg等人[63,128,129]通过一系列的研究证明,当采用C0连续的常数单元对边界进行离散时,需要网格密度每波长十个单元才能确保解的准确性,而采用C1连续的线性插值函数,只需每波长六个单元即可。设水中的声速为1500m/s,则分析频率为300Hz时,网格最大尺寸不能超过0.833m,相对而言更容易满足。
针对以上情况,本文采取试算的方式来确保网格的收敛性。为了降低计算量,采用未充液、未下水的双层壳体模型作为研究的对象,采用不同网格密度计算壳体受力振动的频率响应,对比计算结果,从而找到使解趋于一致的同时密度尽可能小的网格。分别采用映射网格划分方法按三种不同密度生成壳体网格,如图5.9所示,其中1#网格中壳单元最大边长为0.06m,由8616个壳单元组成;2#网格中壳单元最大边长为0.048m,由13600个壳单元组成;3#网格壳单元最大边长0.04m,由18320个壳单元组成。不考虑舷间液体以及壳体外部流场,在内壳中心位置施加单点径向激励。

图5.9 网格密度示意图
Fig5.9 Schematic diagram of mesh densities
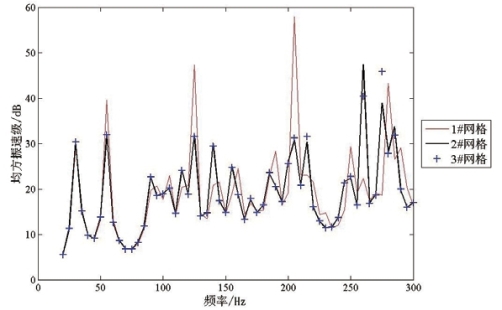
图5.10 不同网格密度外壳均方振速级对比图
Fig5.10 Mean square velocity level of outer layer of shell for different mesh density
图5.10对比了三种网格密度下的外壳表面均方振速级,其中参考振速级为10-6m/s。从中可以看出1#网格与其他两组网格的计算结果差别较为明显,在100-300Hz之间存在多处峰值不一致的情况,而2#网格与3#网格的计算结果吻合较好,除了260Hz与275Hz峰值高度差别达到了7dB外,其他频点处的差别均在1dB以内,因此认为2#网格在本章计算的频率范围达到了收敛,在后续的分析中均采用该网格。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




