如式（4-17）所示，Dirichlet-Neumann区域分解法的收敛判别准则中，e的意义接近于解的误差，但全局迭代法和Schur补方法判定收敛的依据则均为残值，如式（4-24）所示，其中xk为迭代到第k步时得到的近似解。由式（4-24）可见，残值的意义并不等同于近似解与实际解之间的误差。
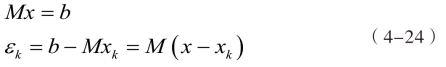
在对算法的计算效率、内存占用量进行讨论前，首先应确保其精确性。为了简化讨论，分别求解单层、双层圆柱壳模型的稀疏网格，并以第二章讨论过的有限元-边界元法配合稀疏LU分解算法所求得的解作为参照对象。设激励力为位于壳体轴向中心位置、双层壳体的外壳上以及单层壳的壳表面处的单点径向激励，幅值为1N；在激励正横方向、距离轴心10m处设置一个声压观察点；设定迭代收敛的判据为ε=10-5。采用Block-Jacobi预条件方法构建全局GMRES求解器的预条件矩阵，如式（4-25）所示。
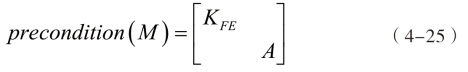
通过C++编程接口调用科学计算可移植扩展工具包PETSc[123]实现了K-Schur、A-Schur和全局GMRES求解器。图4.4和4.5分别对比了不同求解方法在声压观察点处的辐射声压级。
(www.xing528.com)
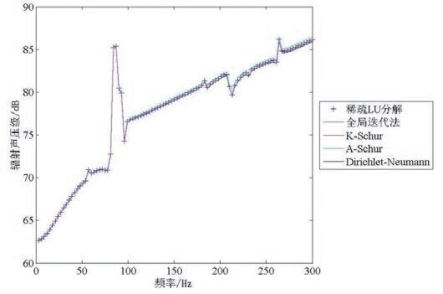
图4.4 求解精度对比图（单层壳体模型）
Fig4.4 Comparison of solvers’ accuracy（single layered cylindrical shell）
图4.4和4.5显示，在ε=10-5条件下，本章讨论的四种迭代方法的计算结果与传统的稀疏LU分解法十分接近，声压观察点处的辐射声压级最大差别约为0.3dB。因此，在后文的讨论中统一将迭代的收敛判别条件设为ε=10-5。
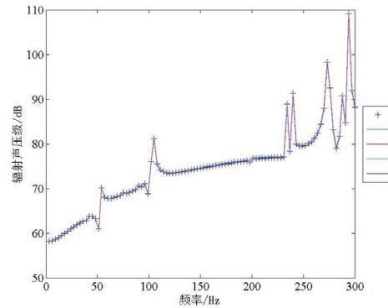
图4.5 求解精度对比图（单层壳体模型）
Fig4.5 Comparison of solvers’ accuracy（double layered cylindrical shell）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
