为了验证ACA边界元法的有效性,分析算法各参数设置对计算精度与效率的影响以及迭代求解器的收敛性能,本节采用球壳和圆柱壳作为验证模型,其中球壳半径为1m,圆柱壳长为2m,半径0.3m,模型外部介质声速为1500m/s,密度为1000kg/m3。模型的形心坐标为(0,0,0),且圆柱壳的轴向与z轴平行。统一设定求解域分割的最小子块含节点数不低于100。
(一)误差阈值e与算法误差分析
如式(3-31)所示,在ACA边界元法中,对矩阵-向量乘法操作的精度产生直接影响的参数是误差阈值e。运算精度随着e的减小而提高,而随之而来的是逼近向量的增加和运算效率的下降。在保证精度的基础上合理的选择ε是本节的研究目标。矩阵-向量乘积的误差函数定义如式(3-40)所示。
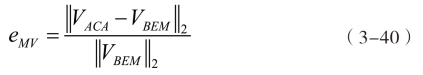
采用映射网格划分方式,将球壳模型离散为866个节点、864个四边形单元组成的网格,300Hz和600Hz频率下的ε-eMV关系曲线如图3.7所示。

图3.7 误差关系曲线(球壳模型)
Fig3.7 Relationship between ε and eMV(spherical model)
采用映射网格划分方式,将圆柱壳模型离散为1090节点,1088个四边形单元组成的网格,300Hz和600Hz频率下的ε-eMV关系曲线如图3.8所示。

图3.8 误差关系曲线(圆柱壳模型)
Fig3.8 Relationship between ε and eMV(cylindrical model)
由图3.7和图3.8可以看出,模型、频率对e与eMV关系的影响较小,取ε=10-6可以确保eMV<1%。
利用映射网格划分方法,将球壳和圆柱壳模型分别划分为602节点、600个四边形单元和746节点、744个四边形单元的网格,设定所有节点沿外法线方向的振速为1,在(10,0,0)出设置一个声压观测点。分别利用传统边界元法和ACA边界元法计算声压观测点处的辐射声压级,结果的误差曲线如图3.9和3.10所示。
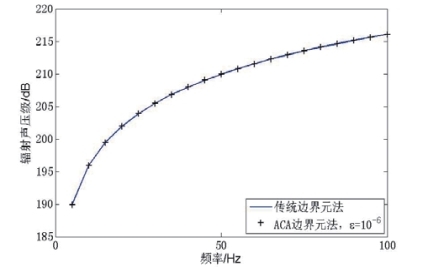
图3.9 球壳模型辐射声压级对比图
Fig3.9 Comparison of radiate sound pressure level for spherical shell

图3.10 圆柱壳模型辐射声压级对比图
Fig3.10 Comparison of radiate sound pressure level for cylindrical shell
(二)压缩率分析
由于ACA算法是通过压缩矩阵数据量来提高矩阵-向量乘法的运算速度,因此可以采用压缩率作为衡量计算效率的指标。压缩率的定义如式(3-41)所示,其数值越小,则说明压缩的效果越好,计算效率也就越高。
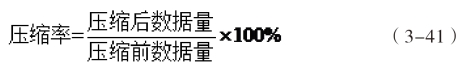
1.频率的影响

图3.11 频率-压缩率曲线(球壳模型)
Fig3.11 Curve of frequency-compression ratio(spherical shell model)

图3.12 频率-压缩率曲线(圆柱壳模型)
Fig3.12 Curve of frequency-compression ratio(cylindrical shell model)
从理论角度看,ACA边界元法计算效率受频率的影响并不明确,为了使后续的讨论不受频率因素的影响,首先观察5Hz-800Hz频段内,压缩率随频率变化的曲线。设定几何相容参数η=0.36,采用PCA方法分割求解域,并利用SVD算法对子块的逼近因子进行重压缩,得到的球壳和圆柱壳模型的频率-压缩率曲线如图3.11、图3.12所示。
由上图可以看出,对于本节讨论的两个模型,ACA边界元法的压缩率受到频率的影响都不超过0.3%,可以忽略不计。
2.几何相容参数的影响
根据文献[69],几何相容参数h的选择对ACA算法的压缩效果影响较大:如果h过小,则某些具有低秩性质的子块将被忽略,而保留了原有的密集形式;如果h过大,则某些不具备低秩性质的子块也被强制的分解,根据式(3-1)可以很容易看出,当k>(m+n)/2时,分解因子的存储量反而大于原有的矩阵子块。
设分析频率为50Hz,采用PCA方法分割求解域,并利用SVD算法对子块的逼近因子进行重压缩,使η在区间(0,1)之内变化,压缩率统计结果如图3.13、图3.14所示。(https://www.xing528.com)
总体而言,矩阵的压缩比对几何相容参数的选择较为敏感。对于长宽比为1的球壳模型,η∈(0.3,0.64)时,均可认为压缩效果达到了最优。而对于长宽比较大的圆柱壳模型,当η<0.3或η>0.8时,ACA算法对矩阵的压缩都会完全失去意义,h的最优区间也只有(0.4,0.56)。要在工程应用中取得良好的效果,应先通过试算确定最优的参数。

图3.13 η-压缩率曲线(球壳模型)
Fig3.13 Curve of η-compression ratio(spherical shell model)
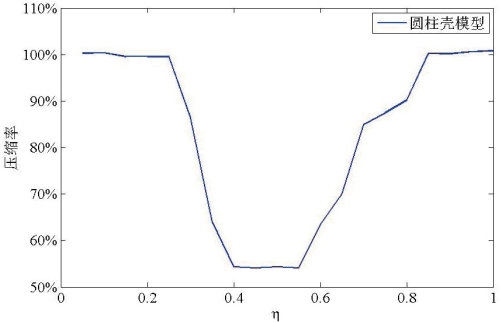
图3.14 圆柱壳模型η-压缩率曲线
Fig3.13 Curve of η-compression ratio(cylindrical shell model)
3.求解域分割方法的影响
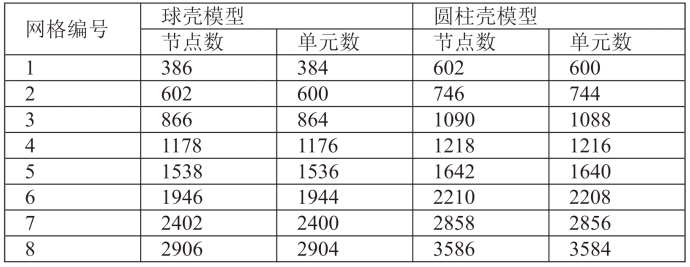
保持网格分割方式不变,按不同密度重划网格,得到网格节点数如表3.1所示。设定η=0.42,计算频率为50Hz,分别采用PCA方法和传统的笛卡尔坐标系方法对求解域进行分割,得到不同模型、不同分割方式下,压缩率随网格规模变化的曲线,如图3.15、3.16所示。
表3.1 网格规模表
Table3.1 Table of mesh sizes
随着节点数量的增加,图3.15和图3.16中的压缩率曲线均呈单调下降的趋势,说明ACA边界元法实现了降低计算复杂度的目的。球壳模型的计算结果显示,PCA分割方法使边界元矩阵的压缩率进一步降低了约10%,而这一改善在圆柱壳模型中更为显著,在某些网格情况下甚至达到了15%,由此可见,PCA方法可以更好适用于不同长宽比的模型问题,改善子求解域之间的几何相容性。
(三)迭代求解器计算效率分析
根据3.2.2小节的讨论可以知道,ACA边界元方程的迭代求解过程可以分为预条件处理和迭代逼近两部分,这两部分各占总求解耗时的多大比例、随频率或网格节点数变化的情况如何,都有待进一步的探讨。
图3.17、3.18和3.19分别为球壳模型的1#、3#、5#网格的预处理时间、迭代逼近耗时和迭代次数的对比图,其中GMRES算法的迭代收敛阈值为10-5。

图3.15 球壳模型压缩率曲线
Fig3.15 Compression ratio curve of spherical shell model

图3.16 圆柱壳模型压缩率曲线
Fig3.16 Compression ratio curve of cylindrical shell model

图3.17 预条件计算耗时曲线
Fig3.17 time consumption of preconditioning

图3.18 迭代计算耗时曲线
Fig3.18 time consumption of iteration
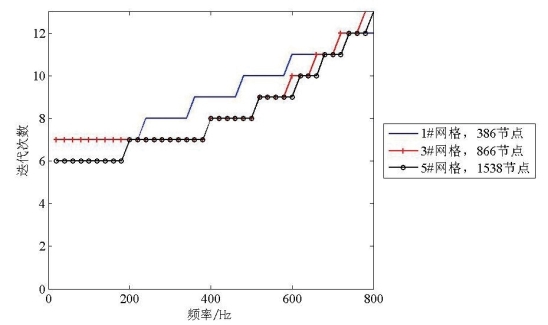
图3.19 迭代次数曲线
Fig3.19 Iteration step number curves
通过对比图中曲线,可以发现:
1)随着频率的升高,预条件计算的耗时并没有出现升高或下降的总体趋势,这与本文采用的稀疏LU预条件算法的性质有关,随着网格节点数由386增长到1538,预条件的计算耗时大约增长为原来的四倍,说明本文所采用的预条件算法的计算复杂度约为O(N)级别;
2)随着频率的变化,迭代求解的收敛速度呈缓慢的下降趋势。在800Hz频率条件下,求解器达到收敛所需的迭代次数和迭代时间均比20Hz频率条件下增长了约一倍;
3)除去频率对迭代收敛速度的影响,随着网格节点数由386增长至1538,单次迭代计算的耗时增长为原来的约5倍。初步验证了ACA边界元法的计算复杂度接近于O(NlogN)。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




