迭代求解水下大型结构边界元方程

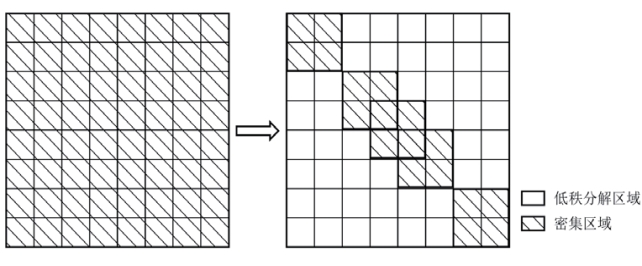
图3.6　ACA算法压缩边界元矩阵示意图
Fig3.6　Compressing BEM matrices with ACA algorithm

如图3.6所示，引入ACA算法使得边界元矩阵的形式发生了变化，除了少数不具备低秩特性的子块外，多数子块都被表达成了低秩逼近因子相乘的形式，一方面无法再利用LU分解等直接方法进行求解，一方面矩阵向量乘法的计算复杂度由O（m*n）降低到了O（n*logn），适宜采用迭代方法。以Gauss-Seidel算法为代表的传统的迭代求解方法虽然不需要矩阵具备显式形式，但在求解非Hermite、非正定的边界元矩阵时通常收敛缓慢甚至是不收敛；Krylov子空间方法是一类求解大型稀疏线性方程组的有效方法，其典型方法包括共轭梯度法（CG）、双共轭梯度法（Bi-CG）、最小残值法（MINRES）和广义最小残值法（GMRES）等，它们所适用的范围各有不同，对于边界元的求解，经验上较为适用的是GMRES。

考虑任意边界元方程Ap=b，则当A的特征值大量聚集于某个特征值附近时（也即，A的谱是聚集的），采用迭代求解算法通常可以迅速获得收敛；与之相反的，若A的谱分布较为分散，则迭代收敛就会变得缓慢，数值稳定性也较差。改善迭代算法收敛性的关键是对方程进行预条件。按照表达形式的不同，可以将预条件技术分为左预条件、右预条件、双侧预条件三类，然而它们对矩阵谱分布的作用并没有本质的区别，这里只考虑最易于实现的左预条件。预条件的一般原理为构建预条件矩阵Ap，使其同时满足：1）易于求逆；2）谱分布与矩阵A尽可能地接近。预条件后的矩阵方程为：

Ap的谱分布与A越是接近，则预条件后的迭代矩阵Ap-1A的谱就越是集中，当Ap=A时显然有Ap-1A=In×n，即迭代矩阵的所有特征值均为1。(www.xing528.com)

对于边界元网格上任意节点子集X，其Chebyshev中心为X0，Chebyshev半径为sX，则对任意σ＞ 0显然有：

参考式（3-10）可以发现，X与其自身之间一定不满足几何相容条件，由此可知，边界元矩阵中对角线上的分块一定不具备低秩特性，在计算中将保持密集形式，而通过将所有不具备低秩特性的子块组装到一起，将得到一个可逆的、非零元呈块状分布的稀疏矩阵Adense。由于几何相容条件背后隐藏了对“强耦合”与“弱耦合”的区分，因此猜测Adense是影响矩阵A谱分布的主要部分，将其作为A的预条件矩阵。

通常情况下，对稀疏矩阵直接求逆，得到的结果矩阵将不具备稀疏性，因此需要采用求解方程Adensex=y替代直接计算x=Adense-1y。考虑到求解边界元方程的过程中，每一次迭代都要重复求解Adensex=y，可以利用稀疏LU分解算法，对Adense进行分解，并在内存中保存分解因子，从而实现“一次分解、多次求解”的目的。