水下大型结构振动预报技术：基于主成分分析的域分割

由于边界元矩阵中的行、列坐标都对应了网格中的各个节点，而矩阵的子块则代表着两个节点子集之间的相互作用，因此要将ACA算法应用于对边界元矩阵的压缩，首先应根据几何相容性条件对求解域进行分割，得到若干节点集，通过将节点集之间的相互作用映射为边界元矩阵中的分块，利用几何相容性条件即可对子块的低秩特性进行预判。

文献中[109-111]较为常用的笛卡尔坐标系分割法，其思路较为简单，即首先找到包围求解域的最小长方体，长方体的各个面均与笛卡尔坐标系的坐标轴垂直，然后沿着三个坐标轴对长方体进行多级等分，直到所得到的子区域足够小或者满足几何相容条件。当求解域为二维空间中的一个圆时，分割结果如图3.3所示。

图3.3　圆形求解域分割示意图
Fig3.3　schematic diagram of splitting circular solving domain

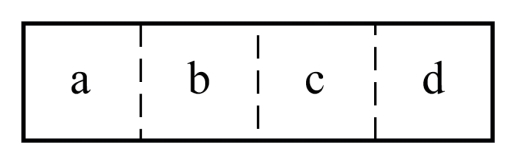
设式（3-10）中的几何相容参数，则由上图可以看出，当包围求解域的长方体接近于正方体时，利用笛卡尔坐标系分割法得到的子块之间几乎都满足几何相容条件。然而当求解域为一个长宽比为4的长方形时，笛卡尔坐标系分割结果如图3.4（a）所示，根据式（3-10）可以推算出，其中a与c、b与d之间均不满足几何相容条件，但如果只沿长方形的长边进行分割，如图3.4（b）所示，则任意两个不同子块之间都满足几何相容条件。由此可见，对求解域的分割方式影响着ACA算法的压缩效果，进而可能影响到ACA边界元法整体的计算效率。

由于实际分析中，我们考察的模型既可能是如图3.3、3.4一样形状规则的，更多情况下也可能是各种不规则的形状，因此必须通过找到一种适应不同形状的求解域分割算法来提高子块间满足几何相容条件的概率。主成分分析[114]（Principle Component Analysis，简称PCA）又被称为主分量分析。利用主成分分析对数据进行处理，可以从影响问题的多个变量中选出影响较大的少数变量，这种思想在图像分析甚至经济学等领域有着广泛的应用。为了说明PCA在分割边界元求解域中的应用，首先考虑一个二维空间中点集z，包含的节点数为n，节点分布如图3.5所示，其中节点i∈[1，n]的坐标记为zi，z的几何中心坐标为Cz，则z的主方向w的定义由式（3-36）给出：

图3.4（a）　笛卡尔坐标系分割示意图
Fig3.4（a）　Subdivision of Cartesian splitting

(www.xing528.com)

图3.4（b）　横向分割示意图
Fig3.4（a）　Subdivision of horizontal splitting

其中v为任意单位向量。在实际计算中可通过计算ZTZ最大特征值所对应的特征向量得到主方向向量w，即：

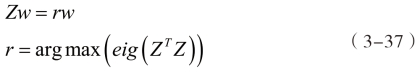
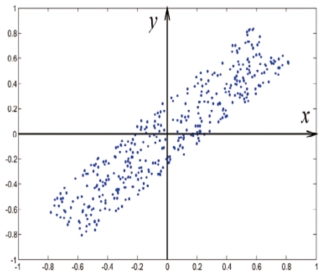
图3.5（a）　笛卡尔坐标系分割
Fig3.5　（a） Subdivision of Cartesian spiting

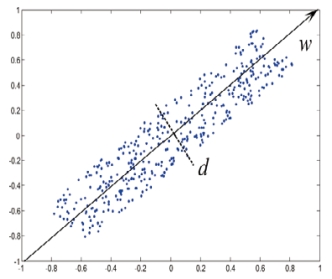
图3.5（b）　主成分分析法分割
Fig3.5　（b） Subdivision of PCA spltting

将w作为坐标轴，得到z中各点的坐标，在坐标值的最大、最小值的中心处取与w垂直的分割面d，将z分割为两部分，如图3.5（b）所示。

在对网格进行逐级分割的过程中，需要重复计算ZTZ及其特征值、特征向量，相对于传统方法引人了额外的计算量，但由于在同一模型的各个分析工况间并不需要重复运算，因此不会对边界元分析的整体计算复杂度造成影响。