如图2.2所示,交叉近似算法的基本思想是从矩阵M的行向量集合U与列向量集合V中迭代的选出影响最大的子集U*和V*,其中U*和V*的元素个数均为k,利用这两个集合作为基,寻求矩阵M的一个最佳逼近M’,使得它们满足式(2-15)的关系。

为了更好地说明自适应交叉算法,本节首先介绍两种较为经典的交叉近似算法:全选主元交叉近似和部分选主元交叉近似算法。

图3.2 交叉近似示意图
Fig3.2 diagrammatic sketch of cross approximation
(一)全选主元交叉近似算法
为了更好地说明自适应交叉算法,本节首先介绍两种较为经典的交叉近似算法:全选主元交叉近似和部分选主元交叉近似算法。
现有非零矩阵M∈Cm×n,且其所有元素的值均为已知。全选主元交叉近似算法首先利用以下步骤找出矩阵M的秩为1的近似矩阵M1:
1)确定M中模值最大的元素所在行、列,记为i1和j1,并设δ=Mi1,j1;
2)取出矩阵M中第i1行和第j1列的向量,存储矩阵U*的第一列u1=M,j1,矩阵V*的第一行v1=Mi1,/δ。
则矩阵M1=U*V*。设整数p:1≤p≤k,设第p步逼近完成后的余项为Rp,则将Rp作为第p+1步逼近的目标,从而形成如式(3-16)所示的关系。

在每一步逼近结束时,都可以利用式(3-17)考察误差阈值是否已经得到满足。
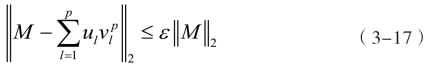
算法3.1 全选主元交叉近似
准备阶段:输入矩阵M,记||M||2=τ,rank(M)=k,设定迭代计数p=1,设定收敛误差阈值ε;
1)当p=1,...,k时,确定矩阵M中模值最大元素所在位置(ip,jp),以及该元素的值δ:=Mip,jp;
2)判别δ,如果δ=0则跳转至步骤6,否则继续执行步骤3;
3)当p≤k时,取出M的第jp列作为和第ip行,利用式(3-18)得到逼近因子向量up和vp:

4)为了节约存储空间,直接更新原矩阵M,使之成为逼近余项矩阵,即:
![]()
5)判别||M||2≤ε*τ,若不满足则令p:=p+1,跳转至步骤1继续循环,否则继续执行步骤6;
6)利用式(3-20)给出矩阵U*∈Cm×p和V*∈Cp×n,算法终止。

据文献证明,若rank(M)=k,则利用算法1进行逼近,经过k次循环后可以得到M的确切分解,即U*V*=M。
通过全选主元交叉近似算法,可以很容易的理解交叉近似的基本原理,但该算法并不具备实际应用价值,原因在于:
1)算法要求矩阵全部元素均为已知,存储矩阵所需的内存空间为O(m*n),而计算矩阵元素的复杂度也不低于O(m*n);
2)每一次循环的开始都要在M中搜索模值最大的元素,该操作的计算复杂度为O(m*n);
3)计算逼近余项矩阵,虽然做到了原地操作,没有额外的内存占用,但仍然要更新M的所有元素,计算复杂度为O(m*n);
4)每一次逼近循环都需要重新计算||M||2,计算复杂度也是O(m*n)。
(二)部分选主元交叉近似算法
较全选主元方法更进一步的是部分选主元法,通过改变搜索逼近向量所在行、列的方式,该方法避免了对M全部元素的需求,同时也降低了更新余项矩阵的计算复杂度。
利用部分选主元的思想,在算法的开始,首先随机选取某一行或一列,在其中找出模值最大的元素,而在循环过程中,每次都根据所选取的行/列各项元素的模值决定下一个逼近向量的选取,从而将选取逼近向量所需的计算复杂度由O(m*n)降低到了线性复杂度O(m)或O(n)。完整的部分选主元交叉近似算法流程如算法2所示。
算法3.2 部分选主元交叉近似算法
准备阶段:输入矩阵M∈Cm×n,记||M||2=τ,rank(M)=k,设定收敛误差阈值e,随机生成整数i1,满足1≤i1≤m,设已使用的行坐标集合D={i1};(https://www.xing528.com)
1)设定迭代计数p=1,计算矩阵M的第i1行向量Mi1,*,确定Mi1,*中模值最大的列坐标j1,即j1=argmax(Mi1,*),以及该元素的值δ:=Mi1,j1;
2)判别δ,如果δ=0则跳转至步骤8,否则继续执行步骤3;
3)计算出M的第j1列,记为M*,j1,利用式(3-21)得到逼近向量u1和v1;

4)判别等式(3-17)是否得到满足,若满足则跳转至第8步,否则使循环计数p=p+1,继续执行步骤5;
5)D:=D⋃{ip},根据列向量up从{1,...,m}/D中选取行坐标ip+1,即ip+1=argmax(up);
6)当p<k时,计算Mip+1,*,计算余项矩阵第ip+1行作为逼近向量vp+1,如式(3-22)所示;

7)令jp+1=argmax(vi+1),根据式(3-23)计算R*,jp+1,取出交叉点的余项值δ=Rip+1,jp+1,若δ=0则终止循环,继续执行步骤8,否则根据(3-24)式计算逼近向量up+1并跳转至步骤4继续迭代;
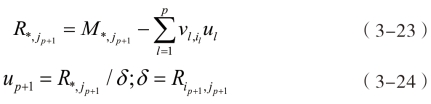
8)利用式(3-25)给出矩阵U*∈Cm×p和V*∈Cp×n,算法终止。

由于将选择模值最大元素的范围由整个矩阵缩小到了余项的特定行、列,部分选主元算法不再要求矩阵M的所有元素为已知,同时也将选择主元的计算复杂度由O(m*n)降低到了O(m)或O(n)级别。此外,由于不再需要余项矩阵R的全部元素,利用式(3-22)、(3-23)计算R的特定行、列,也将更新余项矩阵所需的计算复杂度由O(m*n)降低到了O(m)、O(n)级别。
然而仔细观察算法2的准备步骤,可以注意到其中计算||M||2的计算复杂度为O(m*n),因此该算法仍然没有实现降低运算复杂度级别的目的;此外,算法要求输入矩阵M的秩k为已知,这一点在实现上也存在困难。由此可见,要真正实现更快速的交叉近似算法,还需要寻求一种更为有效的逼近误差估计方法,能够自适应的根据误差阈值给出k的大小。
(三)自适应交叉近似算法
设矩阵M秩为k,利用上文算法1或算法2计算其交叉近似,设第p次迭代结束时近似余项为Rp,则我们可以很容易注意到,对于任意满足1≤p < k的整数p而言,第p+1次迭代的实质都是计算Rp秩为1的交叉近似。利用这一点,可以得到余项矩阵范数与逼近向量之间的关系,如式(3-26)所示
![]()
由此可以利用Frobenius范数估算Rk的绝对误差、相对误差:

由此可去掉交叉近似算法的终止条件中矩阵M的秩k,得到式(3-29)。
![]()
算法3.3 自适应交叉近似算法
准备阶段:输入矩阵M∈Cm×n,记||M||2=τ,设定收敛误差阈值e,定义近似矩阵的Frobenius范数为F0,随机生成整数i1,满足1≤i1≤m,设已使用的行坐标集合D={i1};
1)设定迭代计数p=1,计算矩阵M的第i1行向量Mi1,*,确定Mi1,*中模值最大的列坐标j1,即j1=argmax(Mi1,*),以及该元素的值δ:=Mi1,j1;
2)计算出M的第j1列,记为M*,j1,根据式(3-21)得到逼近向量u1和v1;
3)利用式(3-30)更新逼近矩阵的Frobenius范数;
![]()
4)利用式(3-31)判别逼近是否已经满足误差阈值的要求,若满足则跳转至步骤8,否则继续执行步骤5;
![]()
5)D:=D⋃{ip},根据列向量up从{1,...,m}/D中选取行坐标ip+1,即ip+1=argmax(up),计算Mip+1,*,利用式(3-22)计算余项矩阵第ip+1行作为逼近向量vp+1;
6)令jp+1=argmax(vi+1),根据式(3-23)计算R*,jp+1,取出交叉点的余项值δ=Rip+1,jp+1,若δ=0则终止循环,跳转至第8步,否则利用式(3-24)计算逼近向量up+1;
7)利用式(3-32)更新逼近矩阵的Frobenius范数并跳转至步骤4;
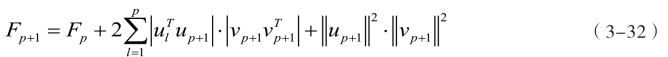
8)利用式(3-25)给出矩阵U*∈Cm×p和V*∈Cp×n,算法终止。
观察算法3的步骤可以发现,自适应交叉近似算法在继承了部分选主元的优点同时,通过引入新的收敛判断策略,避免了直接计算M的范数,真正将算法整体的计算复杂度降低到了线性级别。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




