低秩近似理论在水下结构振动声辐射预报中的应用

（一）矩阵近似的近似逼近

设有一个由积分公式导出的算子表达式L，将L作用于函数f的关系记为Lf，关于Lf的近似化方法研究由来已久，其中最为经典的思想是将L的核函数用退化核来近似表示，并利用加法定理对积分方程中的函数加以处理。著名的快速多极子算法就是直接利用了这种思想，缺点是要求对每一个核函数的显式形式均为已知，使得算法的可移植性较差。近年来发展起来的低秩近似理论则采用算子离散化后得到的矩阵子块作为近似的目标，因此受核函数的影响较小，对不同的物理问题具有更好的适应性。

不论近似的对象是核函数本身还是离散后的矩阵，其目标都是提高积分算子的计算速度，降低存储量。假设一个秩为k的矩阵M∈Cm×n，M的R（k）矩阵低秩近似可用因式分解的形式表示为：

其中U∈Cm×k，V∈Cn×k。式（2-1）也可以更方便的表示为：

经过式（2-1）的分解，存储M所需的内存空间由O（m*n）变为O（k*（m+n）），设有任意向量t∈Cn×1，则利用式（2-1）计算M*t，所需的浮点数乘法操作次数也由O（m*n）变为O（k*（m+n））。如图2.1所示，当M的秩远小于其维数时，利用式（3-1）可以显著降低其存储空间，并提高M*t的运算效率。

图3.1　矩阵分解示意图
Fig3.1　diagrammatic sketch of matrix decomposition

然而在实际应用中，精确的求出M的秩需要较大的计算量，会使得近似失去意义，为此须引入ε-秩以及最佳近似的概念：

其中M的最佳近似矩阵N∈Cm×n，rank（N）=k，||…||代表矩阵的范数。对于给定的秩k，可利用现有较为成熟的算法计算其最佳近似矩阵，而要根据矩阵范数的误差阈值e来确定最佳近似的秩k，最为直接的方法是奇异值分解算法。对矩阵M∈Cm×n进行奇异值分解，结果如式（3-4）所示。

其中U的各列u1，…，un被称为左奇异向量，V的各列v1，…，vn被称为右奇异向量，对角矩阵Σ=diag（σ1，…，σmin（m，n）），σ1 ≥σ2 ≥ σmin（m，n） ≥ 0，σ1被称为M的奇异值。根据奇异值分解的性质，可以得到近似矩阵R：

其中k满足关系σk ≥ε ≥ σk +1，则R作为M的k秩逼近矩阵，满足条件：

其中||…||2代表矩阵的Frobeninus范数。

虽然上述理论较为简单，可以在标准子程序库的基础上加以编程实现，但奇异值分解算法本身的计算复杂度较高，且需要先将原矩阵M每一个元素都计算出来，即使采用部分奇异值分解算法也会使得近似失去意义。

由上述讨论可以看出，要实现对算子L的有效近似，算法应满足以下两点要求：

1）只基于原矩阵的少量元素，不需要计算出整个矩阵；

2）计算分解因子U、V所需的计算量较小。(www.xing528.com)

（二）光滑渐进特性

设有空间Cd中成对的两个不同的点集X={x1，…，xm}和Y={y1，…，yn}，包围它们的最小球形区域分别为DX和DY。设积分函数f：DX×DY→C在X、Y各点上的值组成一个矩阵M∈Cm×n，其中Mi，j=f（xi，yj），1≤i≤m，1≤j≤n。从近似的思想出发，将Mi，j表示为：

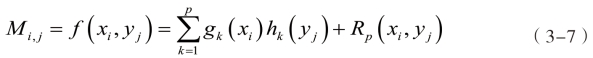
其中p为近似介数，当p→∞，近似余项Rp→0。对于给定的误差阈值εp，应有||Rp（xi，yj）||≤εp。利用上文提到的ε-秩理论，显然有：

快速多极子算法的思想就是根据函数f的性质，导出函数序列gk和hk，从而给出一个形式如式（3-7）的近似等式。虽然具有良好的计算速度，但也直接导致了该算法在可移植性上的不足。

Goreinov等人[112]证明，当f满足渐进光滑特性时，其所导出的矩阵M就具备了有利于引入更为快速的近似方法的性质。

定义2.1（渐进光滑特性）设有一个定于域在Cd空间的函数f（x，y），若存在常数g和c，使得x∈Ω⋅Cd时f满足：

其中α为任意整数，p=|α|，则称f是在Ω内是关于y渐进光滑的。

对于满足渐进光滑特性的函数f，进一步假设存在两个点集X，Y，它们的最小凸包分别为DX和DY，凸包的半径分别为σX、σY，Chebyshev中心分别为X0和Y0，则当X和Y之间满足式（3-10）的关系时，称X和Y是η相容的。

在y0∈Dy处引入泰勒展开，得到：

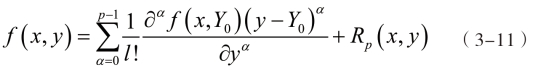
其中展开余项Rp（x，y）定义式为：

有文献证明[113]，展开余项具有如式（3-13）所示的性质。

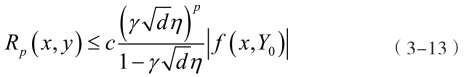
由式（3-13）可以看出，对于在DX上满足渐进光滑特性的函数f，随着展开阶数的增加，展开余项也就是近似误差的幅值是呈指数率衰减的。由此可知，对于给定的误差阈值ε＞0，可依据式（3-14）估计矩阵M的ep-秩近似所需的展开阶数p。

从另一个角度看，低秩近似理论可以很好地应用于具备指数衰减型奇异值分布的矩阵，而实际应用中，绝大多数问题都不具备这样的条件，但利用式（2-10）给出的相容性条件，我们仍然可以判断出系统矩阵中某个子块是否具有低秩特性。