均匀脉动球壳模型的边界元分析成果

为了验证改进的CHIEF方法以及计算程序的有效性，首先分别采用本文方法与解析方法计算均匀脉动球壳的声辐射。模型如图6所示，球心坐标为（0.0，0.0，0.0），球壳半径为1m，球壳的周长划分为40个单元，整个模型共 602个节点，600个四节点四边形单元。流体介质密度为1.0×103kg/m3，声传播速度为1.5×103m/s。

图2.3　球壳模型网格
Fig2.3　Mesh of the spherical shell model

均匀脉动球的声辐射解析解为：

其中r为场点与球心的距离，常数A由下式计算得出：

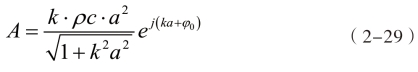
其中a为球半径，ρ为声场介质密度，c为波速，波数k=ω/c，φ0=1/arctan（1/ka）。

将所有节点的法向振速设为10-3m/s，计算在100Hz、300Hz、500Hz和800Hz频率下球壳表面的声压，将所得节点声压解的幅值、相位与解析解对比，误差如图2.4-2.7所示。

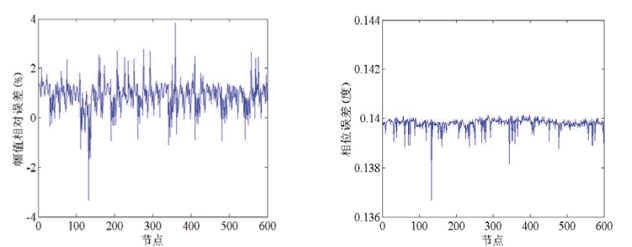
图2.4　100Hz频率下球壳表面声压的幅值误差与相位误差
Fig2.4　Amplitude and phase error of pressure at surface under 100Hz

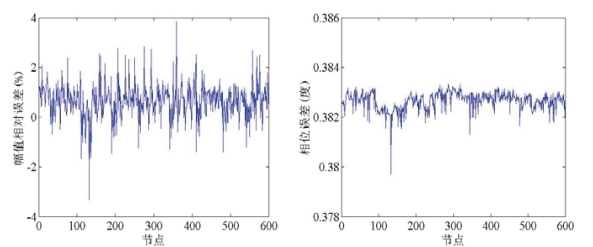
图2.5　300Hz频率下球壳表面声压的幅值误差与相位误差
Fig2.5　Amplitude and phase error of pressure at surface under 300Hz

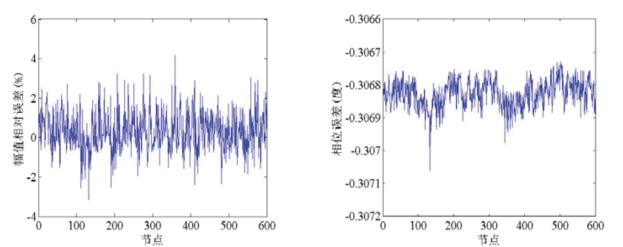
图2.6　500Hz频率下球壳表面声压的幅值误差与相位误差
Fig2.6　Amplitude and phase error of pressure at surface under 500Hz

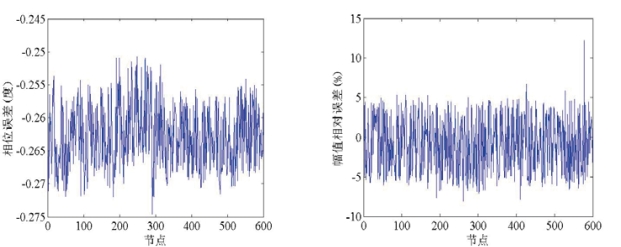
图2.7　800Hz频率下球壳表面声压的幅值误差与相位误差
Fig2.7　Amplitude and phase error of pressure at surface under 800Hz

根据文献[104]，利用常规边界元法处理球形面的辐射问题时，如果波数k与球面半径a满足关系式（2-30）则矩阵出现奇异性，其中n为任意正整数。由此可知，对于半径为1m的球壳，当计算频率为750Hz、1500Hz、2250Hz...时，传统边界元法将出现解不唯一的情况。

为了验证改进CHIEF方法对该问题的处理能力，首先在距离球心10m处设置一个声压观察点，将球壳网格加以细化，得到866个节点、864个单元计算700Hz-800Hz之间球壳表面以及声压观察点处的声压频率响应；进一步细化网格，得到2906个节点，2904个单元，计算1450Hz-1550Hz之间球壳表面以及声压观察点处的声压频率响应。图2.8、2.9分别对比了普通CHIEF方法、改进CHIEF方法和解析方法在两个频段上的计算结果，其中普通CHIEF方法的内点位于球面的中心处。

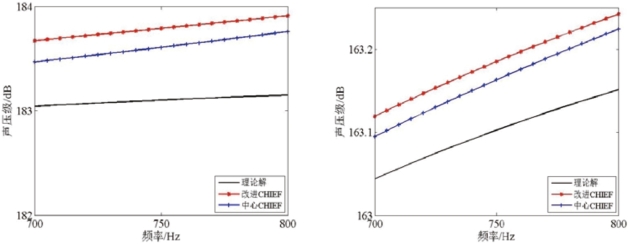
图2.8　700Hz-800Hz球壳表面及声压观察点处辐射声压级对比图
Fig2.8　Comparison of SPL result at surface and field point between 700 Hz and 800Hz

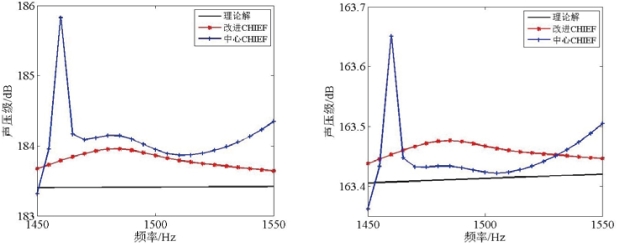
图2.9　1450Hz-1550Hz球壳表面及声压观察点处辐射声压级对比图
Fig2.9　Comparison of SPL result at surface and field point between 1450 Hz and 1550Hz(www.xing528.com)

由图2.8可以看出，三组解的趋势一致，表面辐射声压级的差距在0.6dB以内，由此可知，采用球心作为CHIEF点也能够克服750Hz处矩阵奇异的问题。但在图2.9中，与其他两组解相比，球心CHIEF点的计算结果在1500Hz附近出现了明显的震荡，根据式（2-30）可知，该方法未能克服ka=2π时的矩阵奇异问题。

表2.1　网格节点与单元数表
Table2.1　Number of elements and nodes in mesh sets

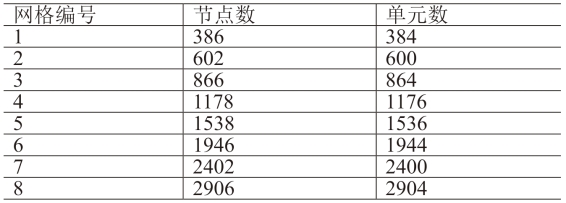
为了检验方法对计算效率的影响，保持网格划分方式不变，分别为球壳模型声场不同密度的8组网格，网格节点数和单元数如表2.1所示，分别采用中心CHIEF法生成矩阵+SVD算法求解、改进CHIEF法生成矩阵+LU分解算法求解，对生成矩阵和求解的计算耗时进行统计。由于LU分解算法和SVD算法的计算效率受矩阵元素幅值的影响极小，生成矩阵的计算量也是固定值，因此只在100Hz频率下的CPU时间进行统计。此外，由于本文所采用的LU分解算法和SVD算法均调用了高度优化的LAPACK库函数[105]，为降低统计结果受程序优化的影响，自编的边界元矩阵生成程序采用OpenMP parallel for指令[106]实现了多线程并行，格林函数的计算调用了Intel MKL[107]相关库函数。

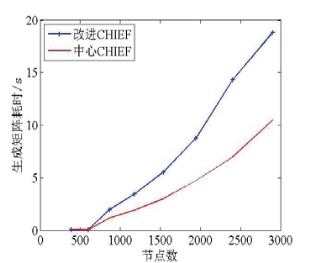
图2.10　生成矩阵耗时对比图
Fig2.10　Comparison of time consumption for constructing matrices

图2.10显示，采用改进CHIEF方法后，生成边界元矩阵的计算耗时增加了接近一倍，与理论预期相符；由图2.11可以看出，对超定方程采用SVD算法，其求解时间随着节点数目的增加而迅速增加，在节点数为386时，求解耗时为LU分解算法的12.6倍，而当节点数达到2904时，这一比例高达26.7倍。综合考虑两部分的计算耗时，本文方法在以上8组网格的计算中，计算效率均优于传统CHIEF+SVD求解法，且随着网格数量的增加，优势更为明显。

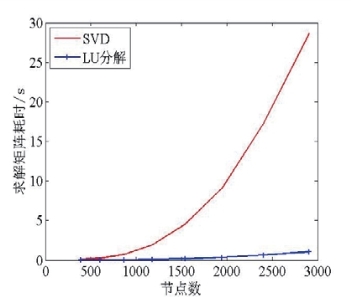
图2.11　求解耗时对比图
Fig2.11　Comparison of time consumption for solving equations

算例2：两侧带球冠的圆柱壳模型。

图2.12　两侧带球冠的圆柱壳示意图
Fig2.12　Sketch map of the capsule like model

为了进一步验证本文边界元程序的有效性，考虑两层带球冠的圆柱壳模型。验证模型为单层胶囊形状壳体，圆柱部分长为1.5m，球壳及圆柱壳半径为1m，划分网格如图2.12所示。另壳体表面各个节点的振速幅值为10-3m/s，设壳体中心位置为坐标系原点，模型轴向为z轴，观察场点坐标为（10.0，0.0，0.0）处的声辐射频响，与SYSNOISE计算结果进行对比。首先计算0～1kHz频带内50个均匀分布的频点，观测点处的声压实部、虚部与幅值如图2.13-图2.15所示。

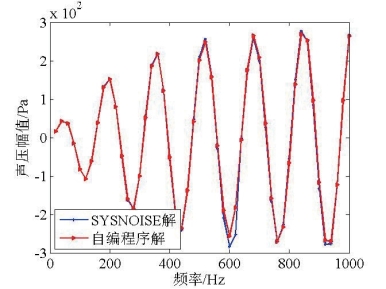
图2.13　辐射声压实部对比图
Fig2.13　Comparison of the real part of sound pressure

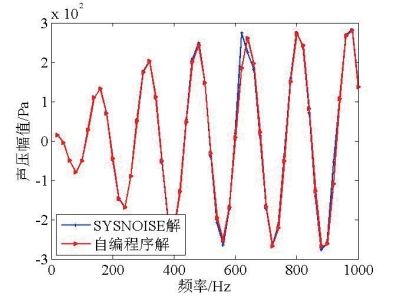
图2.14　辐射声压虚部
Fig2.14　Comparison of the imaginary part of sound pressure

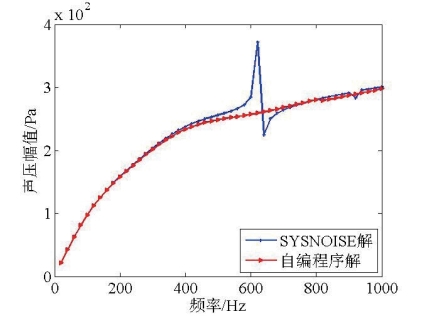
图2.15　辐射声压幅值对比图
Fig2.15　Comparison of the amplitude of radiate sound pressure

通过对比发现在600Hz附近，自编程序与SYSNOISE计算结果差别较大。细化分析频点分布，计算500Hz～800Hz频带内的151个频点的场点声压响应，声压幅值计算结果如图2.16所示。

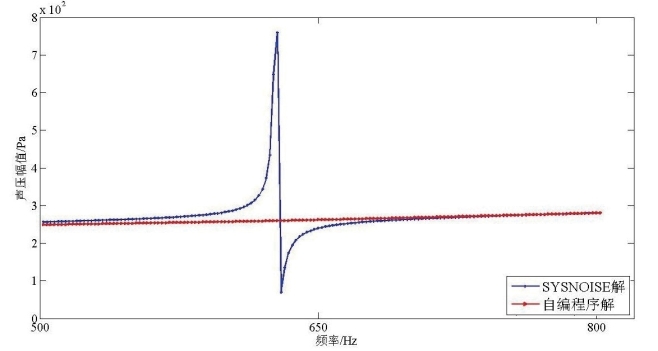
图2.16　500Hz-800Hz声压幅值计算结果对比
Fig2.16　Comparison of the amplitude of radiate sound pressure between 500Hz and 800Hz

由图2.16可以较为清晰地看出，除了600Hz附近SYSNOISE计算结果存在较大的震荡外，两条曲线吻合较好，说明本文提出的改进CHIEF方法可以更为有效的解决边界元矩阵奇异的问题。