声场边界元方程-水下大型结构振动声辐射预报技术引论

如图2.2所示，设一个振动体位于密度为ρ，声速为c的无限流体介质V中，记振动体表面为S，球面Σ为无界声场在无穷远处的边界，因此可以说，体积V是介于无穷远处边界Σ与结构表面S之间的部分，其中的声场满足Helmholtz方程，且在Σ上满足Sommerfeld辐射条件。

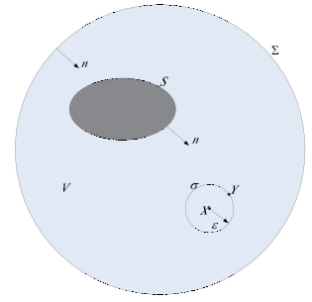
图2.1　外场声辐射问题示意图
Fig2.2　Sketch map of sound radiation problem

现在要计算振动体表面S外的一点X处的声压。声压p是光滑且非奇异的，但是当X=Y时，自由空间的格林函数G将出现奇异性，因此不能直接应用格林第二公式。为了消除这种奇异性，在V内取一小球面将X点包围起来，令球面半径ε→0，于是求解域V-Vσ内可以运用格林第二公式。声压p与格林函数G均满足Helmholtz方程：

由格林第二公式得到上式的等效积分方程：

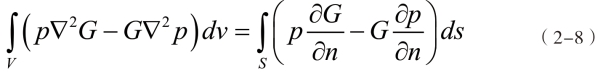
其中G=e-jkr/4πr，r=|x-y|，需要注意的是边界法向的方向应总是指向求解域内部，即在结构表面是指向流体的。上式可变为：

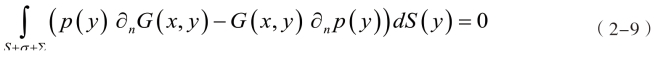
根据Sommerfeld辐射条件得出：

(www.xing528.com)

方程（2-10）描述了体积V中任意一点X处的声压与振动体S面上的声压及声压梯度之间的关系。一旦振动体表面S上的表面声压或声压梯度已知，则可以通过（2-10）式计算出流体域V中任意一点的声压。

图2.3　表面Helmholtz积分示意图
Fig2.3　Sketch map of surface Helmholtz integral

上式给出的是外部 Helmholtz 边界积分方程表达式，当边界上的声压值都已知时，可以直接通过上式求出域内任意一点的声压值。但由于边界上的声压值还不知道，因此，在运用式（2-10）求解场点声压时，须先求出边界上的声压值。为此，需要将X点移到振动体表面上，以求出边界上的声压值。如图2.3所示，X为边界面S上的某个源点。假设振动体的边界面在X点处有唯一的法向向量，这样，我们可以通过在V内取一个半径ε→0的半球面σ将X点包围起来的方法消除当Y→X时所发生的奇异性。得到：

将式（2-11）中声压项和声压导数项分别移动到方程的两端，进行数值离散，记声压沿结构表面的法向导数为q，即可得到矩阵方程：

其中边界元矩阵A、B分别为n×n的方阵，p、q分别为各节点声压及其法向导数的分布向量。由于在频域中，声压的法向倒数与振速之间存在着如式（2-13）所示的线性关系，带入式（2-12）得到辐射面上声压与振速之间的关系方程（2-14）。

式（2-8）既可以用于在已知结构表面振速的条件下求解结构表面声压分布，也可以根据已知的声压分布求解结构表面振速分布。