ANSYS16.1结构非线性分析实例解析

1.非线性结构的定义 

在日常生活中，经常会遇到结构非线性情况。例如，用钉书器钉书，金属订书针将永久地弯曲成一个不同的形状（见图5-1a）；如果你在一个木架上放置重物，随着时间的推移，它将越来越下垂（见图5-1b）；当在汽车或卡车上装货时，它的轮胎和路面间的接触将随货物重量的变化而变化（见图5-1c）。如果将上面例子的载荷变形曲线画出来，可以发现它们都显示了非线性结构的基本特征——变化的结构刚度。 

2.非线性行为的原因

引起结构非线性的原因很多，主要可分为以下3种类型： 

（1）状态变化（包括接触） 

许多普通结构表现出一种与状态相关的非线性行为。例如，一根只能拉伸的电缆可能是松弛的，也可能是绷紧的；轴承套可能是接触的，也可能是不接触的；冻土可能是冻结的，也可能是融化的。这些系统的刚度由于系统状态的改变而突然变化。状态改变或许和载荷直接有关（如在电缆情况中），也可能是由某种外部原因引起的（如在冻土中的紊乱热力学条件）。接触是一种很普遍的非线性行为，是状态变化非线性类型中一个特殊而重要的子集。 

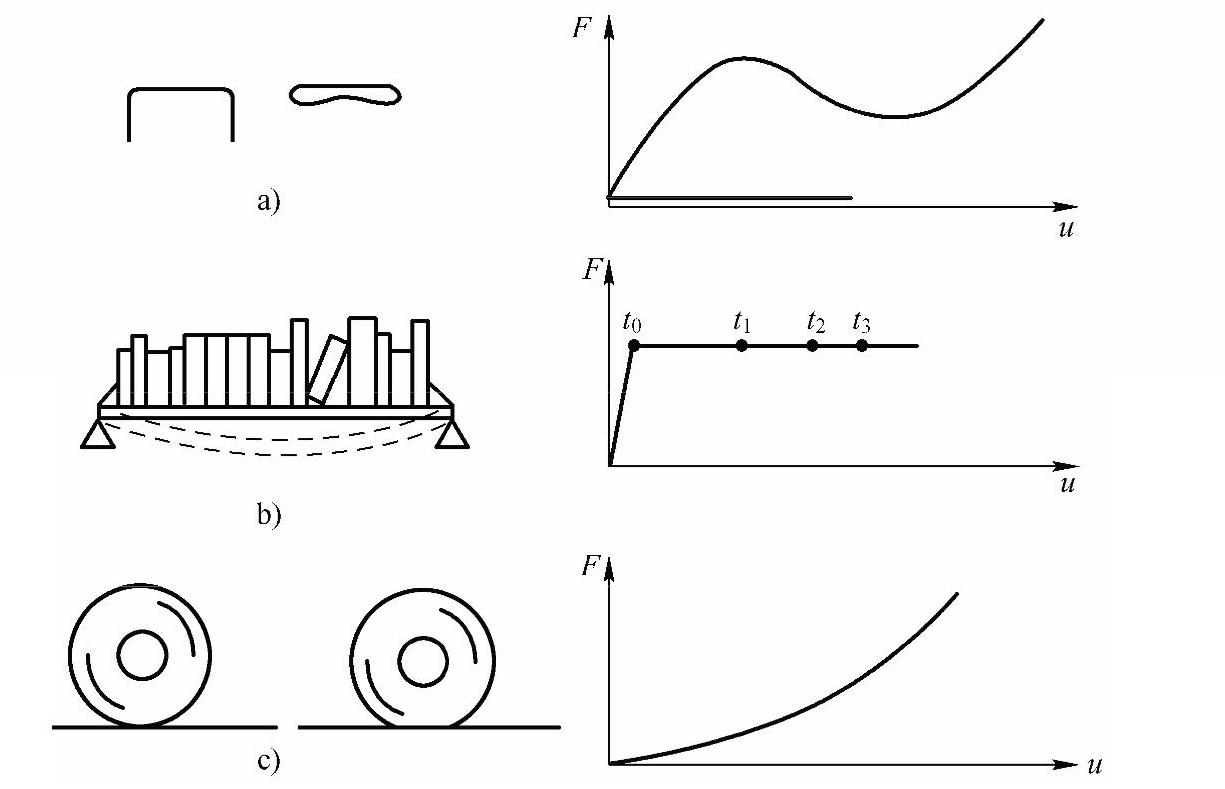
图5-1 非线性结构行为的普通例子

a)Staple b)Book shelf c)Pneumatic tires 

（2）几何非线性 

结构如果经受大变形，其变化的几何形状可能会引起结构的非线性响应。例如图5-2所示的钓鱼杆，在轻微的载荷作用下，会产生很大的变形。随着垂向载荷的增加，杆不断弯曲导致动力臂明显缩短，致使杆在较高载荷下刚度不断增加。 

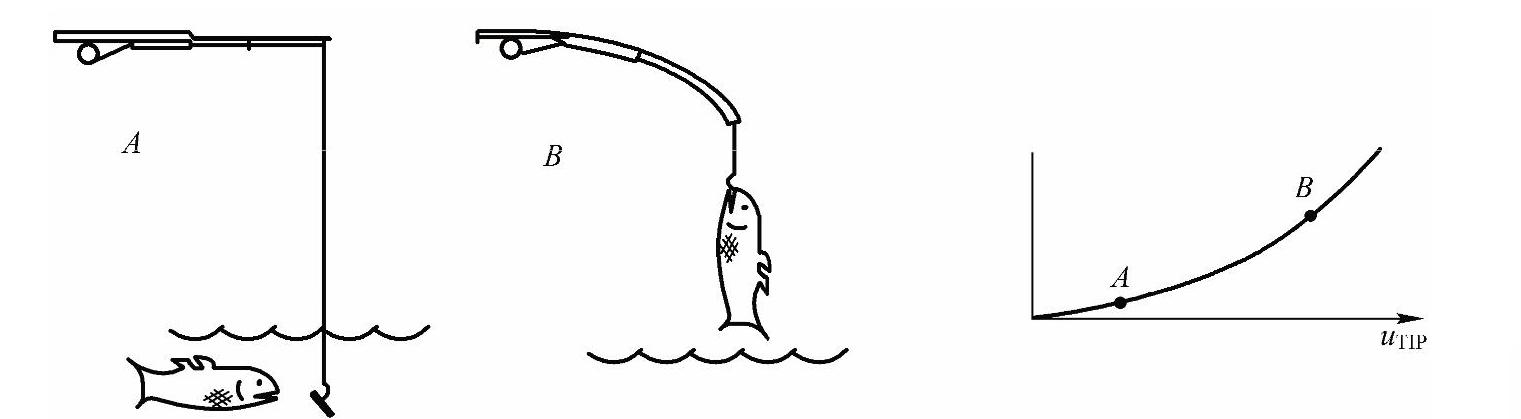
图5-2 钓鱼杆示范几何非线性

（3）材料非线性 

非线性的应力-应变关系是结构非线性的常见原因。许多因素可以影响材料的应力-应变性质，包括加载历史（如在弹-塑性响应状况下）、环境状况（如温度）、加载的时间总量（如在蠕变响应状况下）等。 

3.非线性结构分析中应注意的问题 

（1）牛顿—拉普森方法 

ANSYS程序的方程求解器可以计算一系列的联立线性方程来预测工程系统的响应。然而，非线性结构的行为不能直接用这样一系列的线性方程来表示，需要一系列的带校正的线性近似来求解非线性问题。 

一种近似的非线性求解是将载荷分成一系列的载荷增量。可以在几个载荷步内或者在一个载荷步的几个子步内施加载荷增量。在每一个增量的求解完成后，继续进行下一个载荷增量之前，程序调整刚度矩阵以反映结构刚度的非线性变化。遗憾的是，纯粹的增量近似不可避免地随着每一个载荷增量积累误差，最终导致结果失去平衡，如图5-3a所示。 

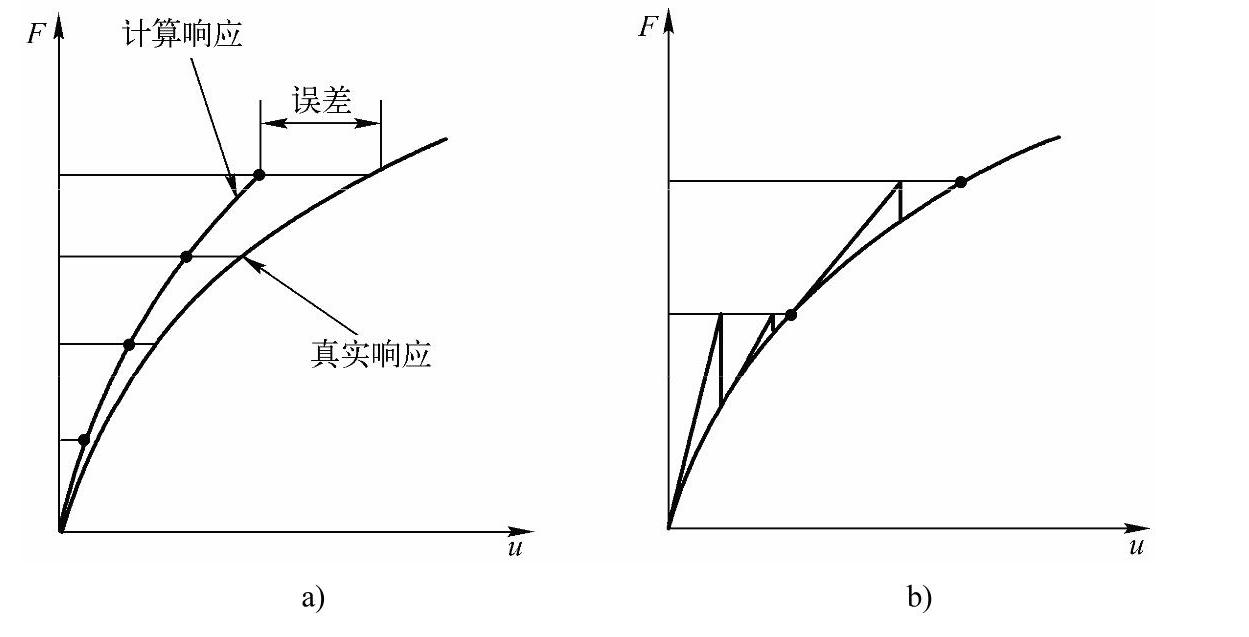
图5-3 纯粹增量近似与牛顿-拉普森近似 

a)纯粹增量式求解 b)牛顿-拉普森迭代求解（2个载荷增量） 

ANSYS程序通过使用牛顿-拉普森平衡迭代克服了这种困难，在某个容限范围内，它使每一个载荷增量的末端解都达到平衡收敛。图5-3b描述了在单自由度非线性分析中牛顿-拉普森平衡迭代的使用。在每次求解前，牛顿-拉普森方法估算出残差矢量，这个矢量是回复力（对应于单元应力的载荷）和所加载荷的差值。之后程序使用非平衡载荷进行线性求解，并且核查收敛性。如果不满足收敛准则，则重新估算非平衡载荷，修改刚度矩阵，获得新解。持续这种迭代过程直到问题收敛。 

ANSYS程序提供了一系列方法来增强问题的收敛性，如自适应下降、线性搜索、自动载荷步以及二分法等，可以采用这些方法来加强问题的收敛性，如果不能得到收敛，那么程序将依据用户指示或者继续计算下一个载荷或者终止。 

对某些物理意义上不稳定系统的非线性静态分析，如果仅仅使用牛顿-拉普森方法，正切刚度矩阵可能变为降秩矩阵，从而导致严重的收敛问题。对于这样的情况，可以激活另外一种迭代方法——弧长方法，来帮助稳定求解。弧长方法使牛顿-拉普森平衡迭代沿一段弧收敛，这样即使当正切刚度矩阵的值为零或负值时，也往往阻止发散。图5-4为这种迭代方法的示意图。 

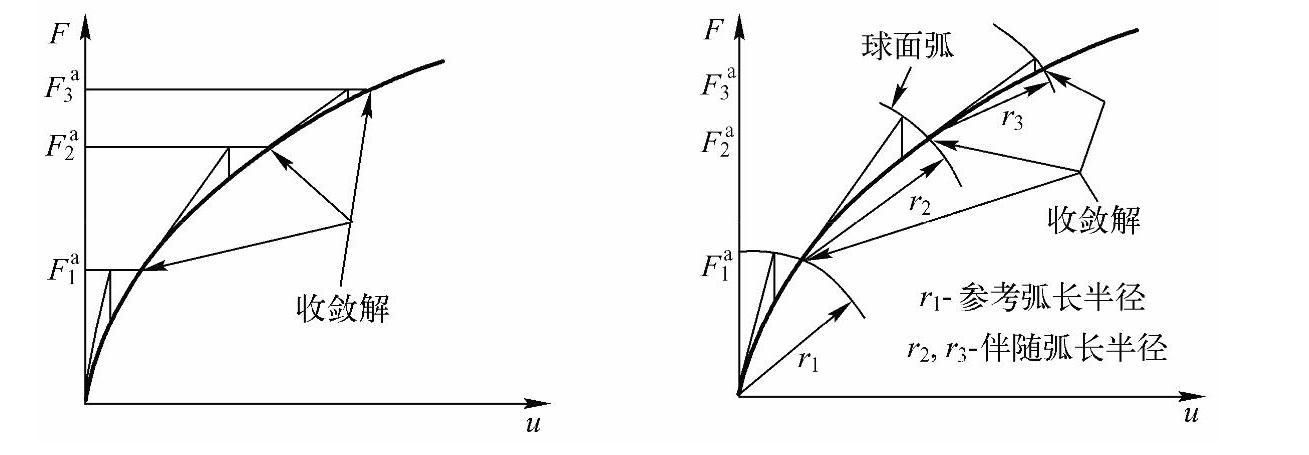
图5-4 传统的牛顿-拉普森方法与弧长方法的比较

（2）非线性求解的操作级别 

非线性求解分成三个操作级别：载荷步、子步、平衡迭代。 

“顶层”级别由在一定“时间”范围内用户明确定义的载荷步组成，假定载荷是线性变化的。 

在每一个载荷步内，通过逐步加载可以控制程序来执行多次求解（子步或时间步）。(www.xing528.com)

在每一个子步内，程序将进行一系列的平衡迭代以获得问题的收敛解。 

图5-5说明了一段用于非线性分析的典型的载荷历史。 

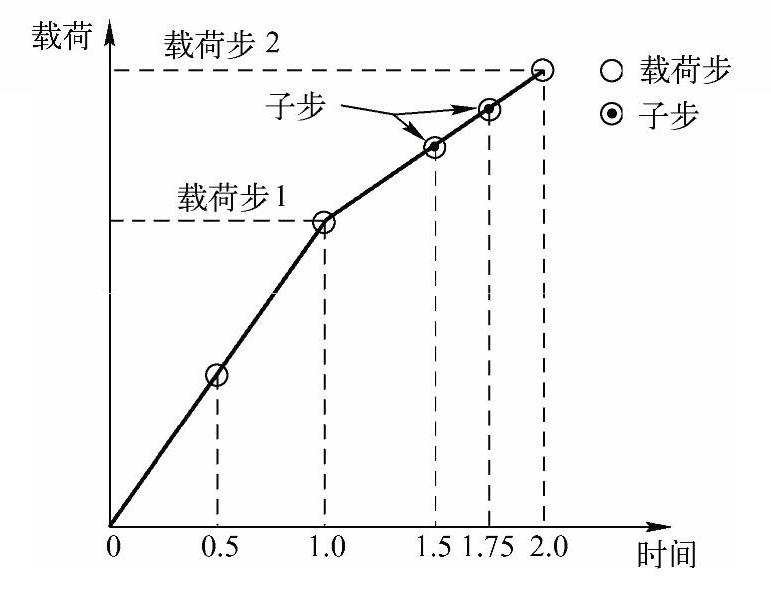
图5-5 载荷步、子步及“时间”

（3）收敛准则 

当确定收敛准则时，ANSYS程序会给出一系列的选择：可以将收敛检测建立在力、力矩、位移、转动或这些项目的任意组合上。 另外，每一个项目可以有不同的收敛容限值。对于多自由度问题，同样也存在收敛准则的选择问题。 

当确定收敛准则时，以力为基础的收敛容限提供了收敛的绝对量度，而以位移为基础的收敛容限仅提供了收敛的相对量度。因此，应当使用以力或力矩为基础的收敛容限。如果需要，可以增加以位移或转动为基础的收敛检查，但是通常不单独使用它们。 

图5-6说明了一种单独使用位移收敛检测导致出错的情况。在第二次迭代后，尽管问题仍旧远离真正的解，但由于计算出的位移很小，很可能被误认为是收敛解。要防止这样错误的发生，应当使用力收敛检测。 

（4）保守行为与非保守行为：过程依赖性 

如果通过外部载荷输入系统的总能量，当载荷移去时系统复原，则称这个系统是保守的。如果能量被系统消耗掉（如由于塑性应变或滑动摩擦），则称该系统是非保守的，图5-7所示是一个非保守系统的例子。 

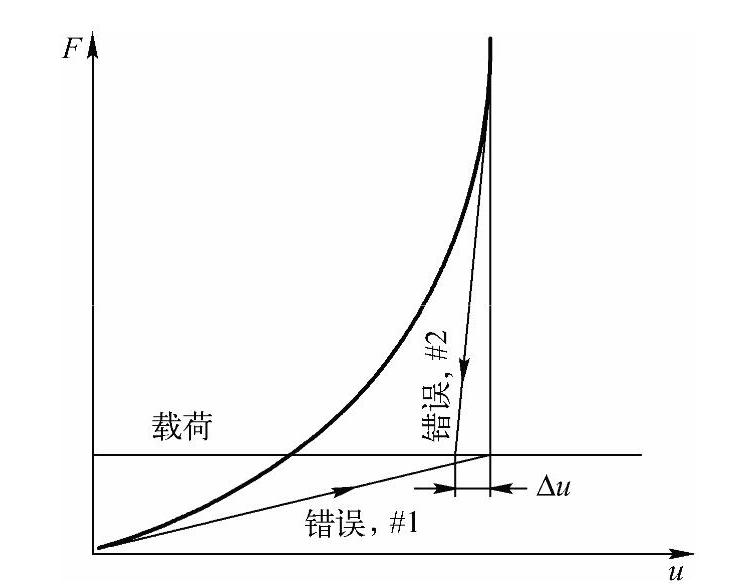
图5-6 完全依赖位移收敛检测产生错误结果显示

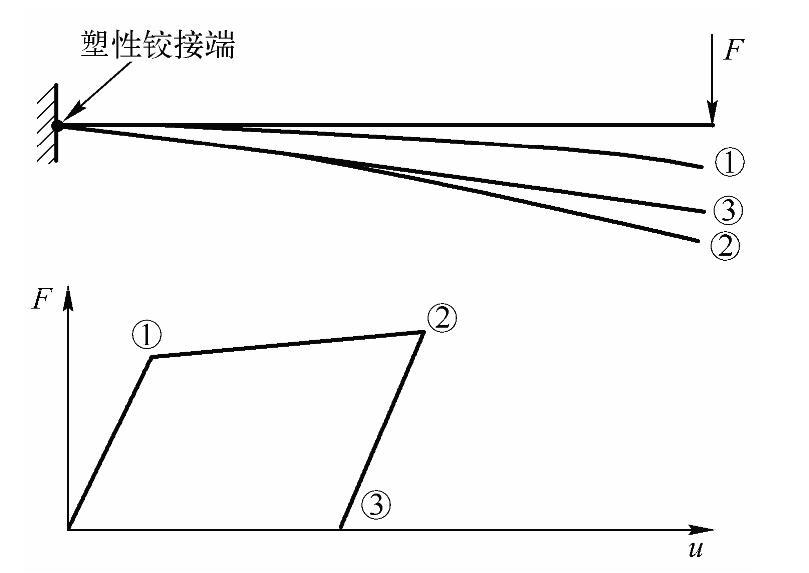
图5-7 非保守（过程相关的）过程

一个保守系统的分析是与过程无关的，通常可以任何顺序和任何数目的增量加载而不影响最终计算结果。而一个非保守系统的分析是过程相关的，必须紧紧跟随系统的实际加载历史，以获得精确的求解结果。过程相关问题通常要求缓慢加载（即使用许多子步）到最终的载荷值。

（5）子步

当使用多个子步时，需要考虑精度和代价之间的平衡：更多的子步骤通常导致较高的精度，但以增加运行时间为代价。ANSYS提供两种方法来控制子步数。

1）子步数或时间步长。

通常可以通过指定实际的子步数，也可以通过指定时间步长来控制子步数。如果结构在整个加载历史期间显示出高度的非线性特点，并且能够确保问题的解答必定收敛，则可以使用任意小的时间步长，并且对所有的载荷步使用这一步长。但要注意的是，必须提供足够大的平衡迭代数以使计算能够达到问题的收敛解。

2）自动时间步长。

ANSYS程序基于结构的特性和系统的响应来调整时间步长。如果结构的行为从线性到非线性变化，或者想要在系统响应的非线性部分期间变化时间步长，就可以激活自动时间步长以便根据需要调整时间步长，获得精度和代价之间的良好平衡。如果不能确保问题成功收敛，则可以使用自动时间分步激活ANSYS程序的二分法。

二分法提供了一种对收敛失败自动矫正的方法。无论何时只要平衡迭代收敛失败，二分法将把时间步长分成两半，然后从最后收敛的子步自动重启动，如果已二分的时间步再次收敛失败，二分法将再次分割时间步长然后重启动，持续这一过程直到获得收敛或到达所设定的最小时间步长。

（6）载荷和位移方向

当结构经历大变形时，应该考虑到载荷的变化。在许多情况中，无论结构如何变形，施加在系统中的载荷保持恒定的方向；而在另一些情况中，载荷将随着单元方向的改变而变化。

ANSYS程序对这两种情况都可以建模。加速度和集中力将不管单元方向的改变而保持它们最初的方向，表面载荷作用在变形单元表面的法向，且可被用来模拟跟随力。图5-8给出了恒力和跟随力的示意图。

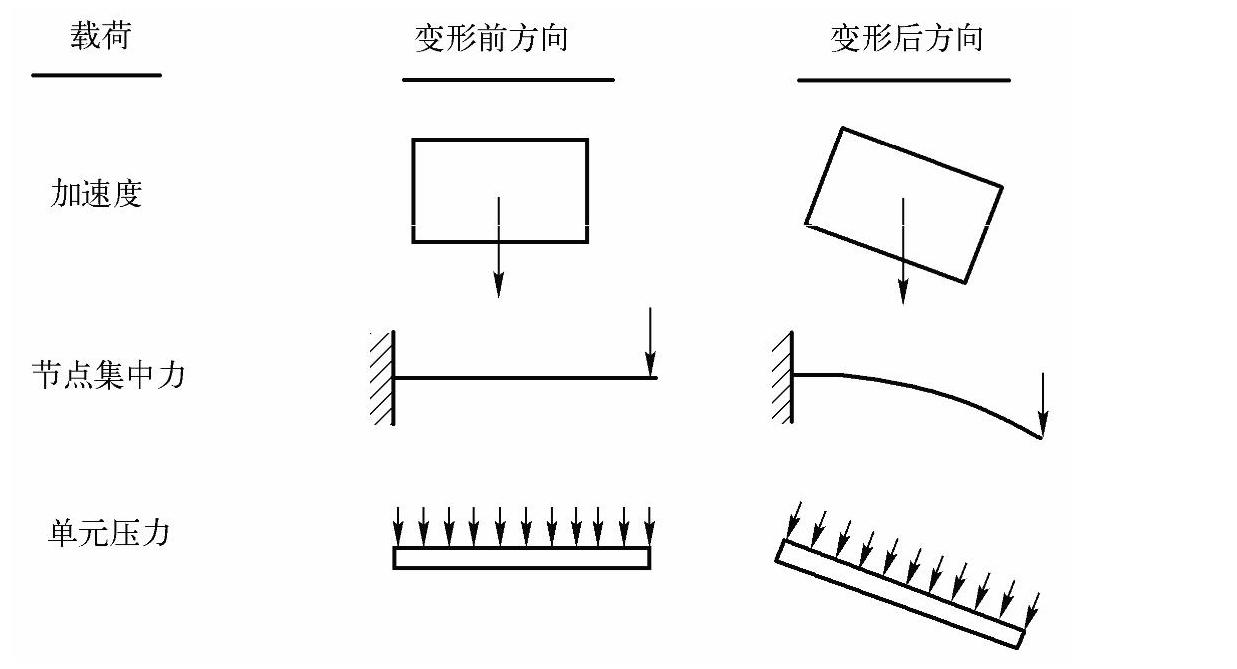
图5-8 变形前后载荷方向

提示：ANSYS在大变形分析中不修正节点坐标系方向，因此计算出的位移在最初的方向上输出。

（7）非线性瞬态过程的分析

用于分析非线性瞬态行为的过程，与线性静态行为的处理相似：以步进增量加载，程序在每一步中进行平衡迭代。静态和瞬态处理的主要不同是在瞬态过程分析中要激活时间积分效应，因此，在瞬态过程分析中，“时间”总是表示实际的时序。自动时间分步和二等分特点同样也适用于瞬态过程分析。