传统集合运算用法-SQLServer数据库基础教程

传统的集合运算都是二目运算。设关系R和关系S具有相同的目n=3，即有相同的属性个数3，且相应的属性取自同一个域。进行并、差、交等集合运算的两个关系必须是具有相同的关系模式，即结构相同，如表1-4和表1-5所示。4种传统的集合运算如图1-5所示。

表1-4 关系R

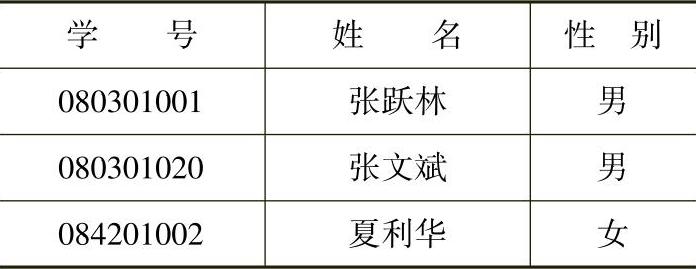
表1-5 关系S

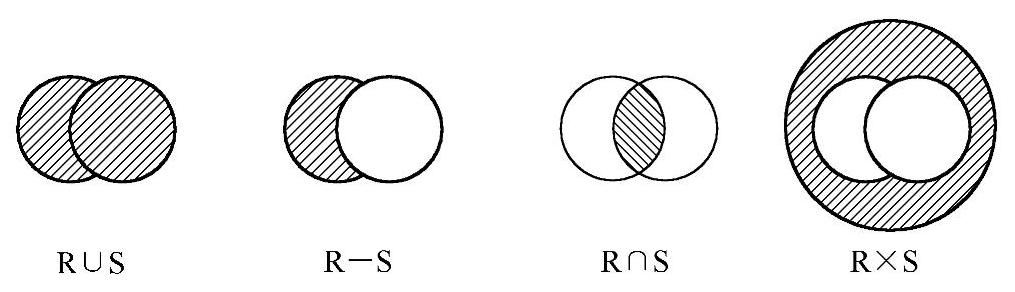
图1-5 传统的集合运算

1.并（Union）运算

设关系R和关系S具有相同的目n（即两个关系都有n个属性），且相应的属性取自同一个域，则关系R与关系S的并由属于R或属于S的元组组成，其结果关系仍为n目关系。

记做：

R∪S={t|t∈R∨t∈S}

其中，t代表元组。

【例1-1】 利用表1-4和表1-5中所示的数据做并运算，得到的结果如表1-6所示。

表1-6 R∪S

2.差（Difference）运算

设关系R和关系S具有相同的目n，且相应的属性取自同一个域，则关系R与关系S的差由属于R而不属于S的所有元组组成。其结果关系仍为n目关系。记做：

R-S={t|t∈R∧t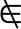S}

【例1-2】 利用表1-4和表1-5中所示的数据做差运算，得到的结果如表1-7所示。

3.交（Intersection）运算

设关系R和关系S具有相同的目n，且相应的属性取自同一个域，则关系R与关系S的交由既属于R又属于S的元组组成。其结果关系仍为n目关系。记做：(www.xing528.com)

R∩S={t|t∈R∧t∈S}

【例1-3】 利用表1-4和表1-5中所示的数据做交运算，得到的结果如图1-8所示。

表1-7 R-S

表1-8 R∩S

4.广义笛卡尔乘积（Extendedcartesianproduct）

（1）什么是笛卡尔积

在数学中，两个集合X和Y的笛卡尔积（CartesianProduct），又称直积，表示为X×Y，是其第一个对象是X的成员而第二个对象是Y的一个成员的所有可能的有序对：

X×Y={（x，y）|x∈X∧y∈Y}

笛卡尔积得名于笛卡尔，他的解析几何的公式化引发了这个概念。

具体的说，如果集合X是6个元素的点数集合{A，K，5，4，3，2}而集合Y是4个元素的花色集合{♠，♥，♦，♣}，则这两个集合的笛卡尔积是24个元素的标准扑克牌的集合：

{（A，♠），（K，♠），…，（2，♠），（A，♥），（K,♥），…，（2，♥），（A，♦），（K，♦）…，（2，♦），（A，♣），（K，♣），…，（2，♣）}。

（2）广义笛卡尔乘积运算

数学家将关系定义为一系列域上的笛卡尔积的子集。这一定义与表的定义几乎是完全相符的，把关系看成一个集合，这样就可以将一些直观的表格以及对表格的汇总和查询工作转换成数学的集合以及集合的运算问题。

关系R为n目，关系S为m目，则关系R和关系S的广义笛卡尔积为（n+m）目元组的集合，记做：R×S={⌒t_rt_s|t_r∈R∧t_s∈S}。

元组的前n个分量是关系R的一个元组，后m个分量是关系S的一个元组。

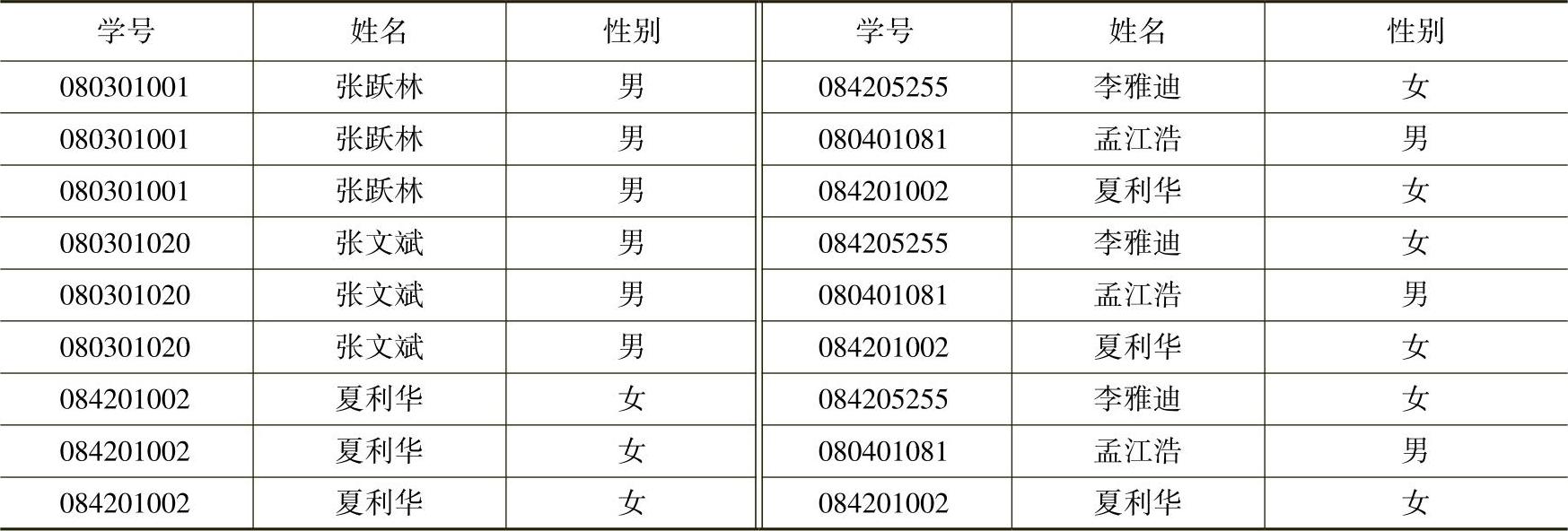
【例1-4】 利用表1-4和表1-5中所示的数据做广义笛卡尔积，其结果如表1-9所示。

表1-9 R×S