物联网实验教程：椭圆曲线与群组密钥协商方法简介

1.定义

给定一个域F，方程

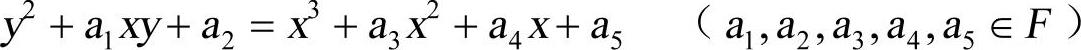
所确定的平面曲线外加一个无穷远点共同构成F上的椭圆曲线，通常用E表示，该方程称作Weierstrass方程。若F的特征大于3，则通过坐标变换可将上述方程化简为

y²=x³+ax+b

2.运算法则

设P，Q，R为椭圆曲线上的点，∞为无穷远点，E（F）为椭圆曲线上所有点的集合，有限域F上的椭圆曲线满足以下运算法则：

若P（x，y）∈E（F），则P+∞=∞+P=P，∞=-∞；

若P（x，y）∈E（F），则P+（-P）=∞，-P=-（x，y）=（x，-y）；

若P（x₁，y₁），Q（x₂，y₂）∈E（F），P，Q连线的延长线交椭圆曲线于点R关于x轴的对称点，则P+Q+R=∞，即P+Q=-R，如图5-2所示。

图5-2 P+Q=-R

3.椭圆曲线离散对数问题

若k∈Z，E（F）为椭圆曲线，P（x，y）∈E（F），定义点乘kP如下：

当k＞0时，kP=P+P+L+P（共k个）；

当k＜0时，kP=（-k）（-P）；

当k=0时，kP=∞；

若存在最小的正整数n使得nP=∞，则称n为点P的阶。(www.xing528.com)

已知k和kP，求解k的问题称为椭圆曲线离散对数问题（ECDLP）。当点P的阶为大素数时，ECDLP的计算是不可行的（即椭圆曲线离散对数问题的难解性）。

4.固定轮数群组密钥协商方案

在无线传感器网络中，节点簇的各节点之间的通信是一种群组通信的方式。为了保证节点簇通信的安全，在一种可认证的群组密钥协商协议基础上，结合椭圆曲线密码系统，使用基于椭圆曲线的固定轮数的群组密钥协商协议构建协商方案。该方案轮数固定，可扩展性强；轮数固定，两轮协商可得出群组密钥，简单高效。群组密钥协商方案如下：

（1）第1轮协商

设有n个用户U₀，U₁，L，U_n-1参与群组密钥协商。

1）每个用户U_i，0剟in-1，随机选取r_i∈_RZ_q^*，计算Z_i=r_iP，其中，r_i为第i个用户产生的随机数，P为预先在椭圆曲线上取的一个公共点。

2）将Z_i发送给用户U_{（i-1）modn}和U_{（i+1）modn}。

（2）第2轮协商

1）每个用户收到Z_{（i-1）modn}=r_{（i-1）modn}P和Z_{（i+1）modn}=r_{（i+1）modn}P后，计算X_i=（Z_{（i+1）modn}-Z_{（i-1）modn}）×r_i，并将X_i广播到每个用户。

2）每个用户U_i计算它们的会话密钥。

3）K_i=nr_iZ_{（i-1）modn}+（n-1）X_i+（n^-2）X_{（i+1）modn}+L+X_{（i-2）modn}

正确性证明：对于任意的第i个用户，其计算出的密钥为

那么，对于第i-1个用户计算出来的密钥为

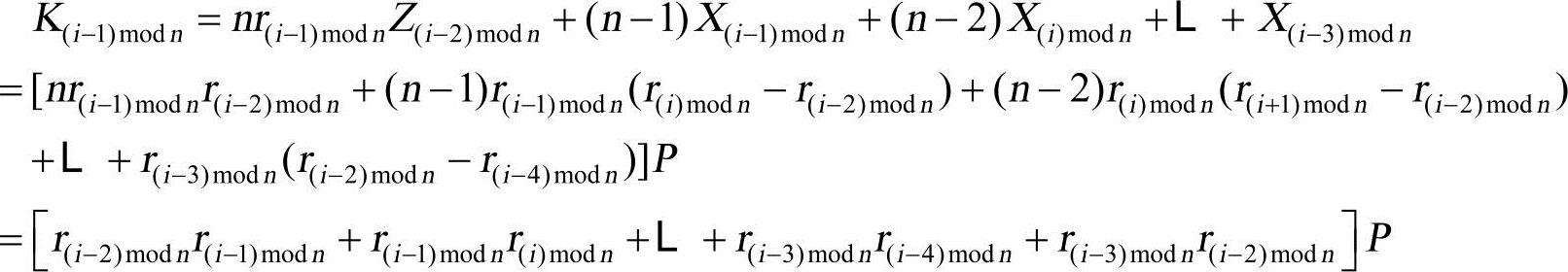
显然，K_i=K_{（i-1）modn}。