数字通信里传输的数据,经常会出现很多连“0”和很多连“1”的情况。这不利于接收端恢复时钟。有一种解决方式,就是对输入的串行数据加扰,这就是扰码。加扰是根据一定的运算算法来操作的,加扰以后的数据,也就是扰码,“0”和“1”交替出现,很容易提取时钟。因此,我们通常也把扰码这种编码方式作为形成随机数据的一种方法。
扰码的实现方法,本质上是利用了循环的移位寄存器,移位寄存器的结构是由扰码生成多项式来决定。而通常扰码生成多项式,则使用的是ITU-T推荐的扰码算法。该组织推荐的用于SDH的扰码生成多项式可以表示如下:X7+X6+1。
扰码器(加扰器)的设计
假设扰码的输入串行数字序列为Tk,输出为Sk。
根据上面这个多项式,意味着加扰之后的数据输出和输入序列关系为:Sk=Tk^X6^X7。
图17.35是扰码器的结构示意图。图中圆圈中有个加号的这个符号表示异或运算。
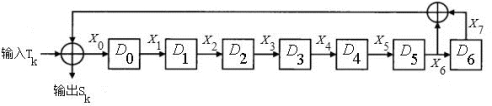
图17.35 扰码器的结构示意图
下面这段程序就是扰码器的描述。
例17.25:扰码器的描述。


该扰码程序是可以综合通过的。图17.36是综合的RTL视图。
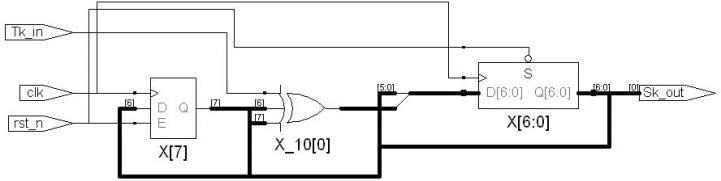
图17.36 扰码器综合的电路
解码器的设计
加扰以后的输出就是Sk,这个信号经过传输以后到达接收端,作为接收端的解扰器的输入。所以我们也假设解扰器的输入为Sk,输出为Rk。
解扰器的输出序列和输入序列的关系为:Rk=Sk^X6^X7=Tk^X6^X7^X6^X7=Tk。这个公式用到的原理就是一个数和另外一个数异或两次,结果就是这个数本身。比如Tk和X6异或了两次,结果就是Tk本身。
图17.37是解扰器的结构示意图。
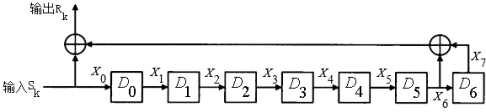
图17.37 解扰器的结构示意图
下面这段程序就是解扰器的描述。
例17.26:解扰器的描述。

该程序也是可以综合通过的。图17.38是综合的RTL视图。结构很清晰。
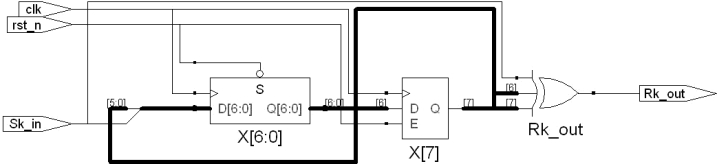
图17.38 解扰器综合的电路
在通信课程涉及加扰和解扰的内容时,如果想着用单片机或者DSP,甚至是用分立元件的方式来开发加扰、解扰电路,你会感觉有点束手无策。也不是说用那些技术一定做不了,而是觉得即使是做出来了,过程也会很麻烦。但是,经过上面的这两个加扰、解扰的例子,我们可以看到,简简单单的两段程序,就能把ITU-U推荐的多项式算法解释清楚,而且还在开发环境完成了语法调试和综合。这就是FPGA硬件描述语言开发技术的优点。
并行加扰器的设计(https://www.xing528.com)
高速速率传输的时候,数据处理的要求很高,所以一般扰码器和解扰器都不是串行的,而是采用并行的方式。对于循环移位寄存器,存在着如下的关系:
![]()
读者要清楚,上式的+表示异或的意思。于是我们就可以列出![]() 之间的关系,并以矩阵的形式表示出来,即
之间的关系,并以矩阵的形式表示出来,即
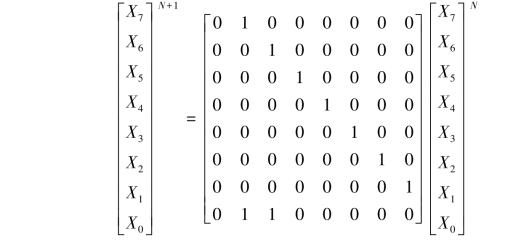
令矩阵![]() ,如果是8位输入的并行数据,要想知道N+8时刻输出与N时刻输出之间的关系,就得把上式等式右边的矩阵系数取8次自己乘以自己,即
,如果是8位输入的并行数据,要想知道N+8时刻输出与N时刻输出之间的关系,就得把上式等式右边的矩阵系数取8次自己乘以自己,即

上面这个矩阵系数最后一行第三列的2意味着异或了同一个数两次,根据异或的特性,相当于没有对这个数异或,于是上式可以变为

因此我们可以得到

我们将以上面这3个公式作为并行扰码的理论分析基础来进行下面的论述。
假设并行的8位输入的数据是Tk_in[7:0],扰码器的并行的8位的输出数据为Sk_out[7:0],X[6:0]是加扰移位寄存器的初始状态,假设加扰器复位后初态为X[6:0]=7’b111_1111(复位后初态不能为全0),于是可以得到并行输出和并行输入、移位寄存器初态之间的关系,如下:

例17.27:8位输入的并行加扰器的描述。


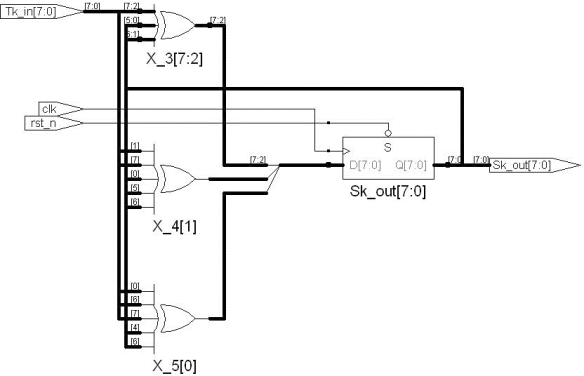
图17.39 并行加扰器综合的电路
并行解扰器设计
假设Sk[6:0]是并行的8位输入给解扰器的数据,X[7:0]是移位寄存器的各位的状态,Rk[7:0]是并行的从解扰器输出的数据。经过推导后,也可以得到输入给解扰器的并行数据、寄存器状态、解扰器的并行数据输出之间的关系,如下:

例17.28:并行解扰器的描述


ISE综合的RTL视图如下所示。
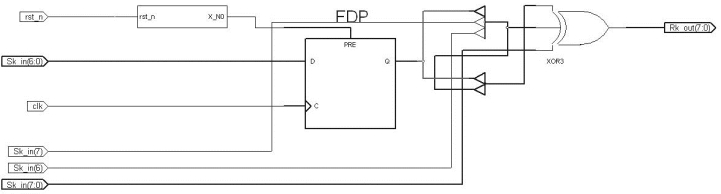
图17.40 并行解扰器综合的电路
上图中,移动鼠标到很粗的黑线上,显示它形成了总线(bus tap)了。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




