基于LFSR的伪随机数生成方法改为FPGA系统设计

有时候，在FPGA的开发中需要一些随机数。其中用的比较广泛的一种产生随机数的方法是线性反馈移位寄存器（LFSR）。

它的结构包括n个D触发器和一些异或门，如图17.25所示：

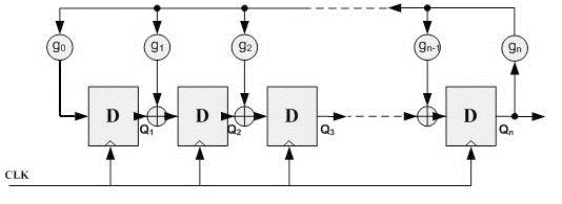
图17.25　线性反馈移位寄存器示意图

其中，GN是反馈系数，它们的取值只能是0或1。GN取为0时表明不存在该反馈支路，GN取为1时表明存在该反馈之路。N个D触发器意味着最多可以提供2^N-1个状态（不包括全0的状态）。如果要保证这些状态没有重复，GN的选择上应该满足一定的条件。

下面，我们以N=3，G0=1，G1=1，G2=0，G3=1为例，介绍一下LFSR的基本情况。以上参数的LFSR的结构如图17.26所示：

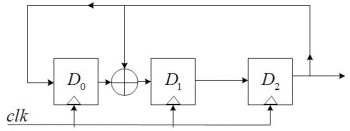
图17.26　线性反馈移位寄存器实例图

假设，最初D2 D1 D0=111。我们把这个最初的值叫作种子（SEED）。下一个时钟触发的作用下，可以得到：

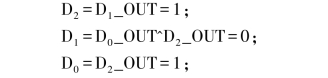
也就是，D2D1D0=101；同理，再下一个时钟的触发下，可得到D2D1D0=001。

我们把依次的状态转移图绘制如图17.27所示：

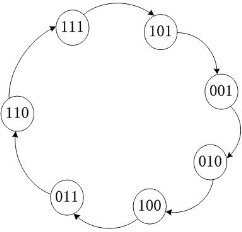
图17.27　线性反馈移位寄存器状态转移图

从图17.27可以看出，正好有2^3-1=7种状态，不包括全0。

我们得到如下三条结论：

（1）最开始的状态由SEED决定，而且一定要给状态的循环提供这个种子SEED；

（2）反馈系数不同，意味着可以得到不同的状态转移图。但是有个条件，就是必须保证GN等于1，否则没有反馈；

（3）越多的D触发器的个数，意味着可以产生的状态就越多，也就越“随机”。

总结一下：我们可以通过一定的算法（比如给定不同的反馈系数）搭配事先给定的随机种子（seed），经过运算后可以得到一个周期循环的序列。在这组序列中以相同的概率选取其中一个数字，该数字可以被称作伪随机数。当然，该所选数字并不是真正意义上的具有完全的随机性的数字。但是从实用的角度来讲，其随机性已经足够了。由于这个随机数是按照一定算法模拟产生的，其结果是确定的，是可见的，因此并不是真正的随机数。所以我们称之为“伪”。伪随机数的选择是从随机种子开始的，所以为了保证每次得到的伪随机数都足够的“随机”，随机种子的选择就显得非常重要，如果随机种子一样，那么同一个随机数发生器产生的随机数也会一样。

例17.22：取系数N=3，G0=1，G1=1，G2=0，G3=1，利用LFSR生成一个3位的伪随机数。(https://www.xing528.com)

图17.28是仿真的波形：

图17.28　LFSR生成3位伪随机数实例的仿真波形

仿真图中，在第2个clk的下降沿末期，给load置数“1”，于是从下一个clk上升沿开始，rand_num依次输出伪随机序列“011-110-111-101-001-010-100”。

我们做一下扩展。当N=8，反馈系数为G0G1G2G3G4G5G6G7G8=101110001时，设计一个基于LFSR的伪随机数发生器。该如何做？

可知，它共有2^8-1=255个状态，其LFSR的结构如图17.29所示：

图17.29　LFSR生成3位伪随机数实例的结构

下面是它的程序：

如果以1111 1111为种子，在把LOAD信号置位后，循环输出开始，一共有255个状态，依次为255、143、111、222、205、235......

例17.23：前面的例子里，我们取系数N=3，G0=1，G1=1，G2=0，G3=1，并利用LFSR生成了一个3位的伪随机数。在本例中，将该模块改写为函数的形式。

因为LFSR是移位寄存器，移位寄存器最大的特征就是使用非阻塞赋值。

在最前面的例子里，我们确实使用了非阻塞赋值。

但是若要改写为函数形式的话，由于在函数里不能采用非阻塞赋值，因此，在上面这个例子的函数里，我们引入了一个临时寄存器变量temp，将rand_num的三个位先暂存了一下。这就解决了移位寄存器应该使用非阻塞赋值的难题。