格雷码是以它的发明人弗兰克·格雷命名的一种编码方式。最初发明于1953年,用于通信的目的。我们知道,任何一段信息,如果简单的翻译为最原始的二进制对应形式发送出去,而不加以编码转换,则必然在效率、保密性和实际使用上出现问题。我们一般把格雷码也叫作循环二进制码,或者反射二进制码。格雷码有个特点:就是任意的相邻的代码只有一位二进制的区别。比如从十进制的8变化到9,相应的格雷码为从1100变化到1101,只有最右边第四位的区别。这个特点很重要。为什么说这点很重要呢?要知道,格雷码从一个数变化为相邻的另一个数时,只有一个数据位有变化,意味着它可以尽量避免出现二进制编码电路里经常会有的亚稳态现象。
格雷码可以被用在很多诸如FIFO、RAM地址寻址和计数器等场合。
下面,我们看一下格雷码表。常见的自然二进制、十进制和格雷码的关系如表17.1所示:
表17.1 格雷码表

格雷码也是二进制码。我们最初学习的从十进制转化为的那个二进制叫作自然二进制,相应的码叫作自然二进制码,简称二进制码。格雷码叫作二进制格雷码,简称格雷码。
那么,二进制码与格雷码之间是按照什么规则进行转化的呢?
二进制码转换成格雷码
二进制码转换成格雷码,其规则是:
(1)二进制码的最高位保留,将其作为格雷码的最高位;
(2)次高位格雷码为二进制码的高位与次高位相异或;
(3)格雷码其余各位与次高位的求法相类似。
例17.17:
假设有二进制码为bn-1 bn-2 bn-3...b2 b1 b0
假设其对应的格雷码为gn-1 gn-2 gn-3...g2 g1 g0
那么规则是:
(1)保留最高位,即gn-1=bn-1;
(2)其他各位为:gi=bi+1⊕bi,i=0,1...,n-2,符号⊕表示异或的意思。
图17.17举了一个例子,从二进制码11010转化为格雷码10111。
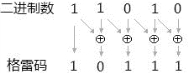
图17.17 二进制码11010转化为格雷码10111的原理
格雷码转换成二进制码
格雷码转换成二进制码,其规则是:
(1)格雷码的最高位保留,将其作为二进制码的最高位;
(2)次高位二进制码为高位二进制码与次高位格雷码相异或;
(3)二进制码的其余各位与次高位二进制码的求法相类似。
例17.18:
假设有格雷码为gn-1 gn-2 gn-3...g2 g1 g0(https://www.xing528.com)
假设其对应的二进制码为bn-1 bn-2 bn-3...b2 b1 b0
那么规则是:
(1)保留最高位,即bn-1=gn-1;
(2)其他各位为:bi-1=gi-1⊕bi,i=1,2,3,...,n-1。
图17.18举了一个例子,从格雷码10111转化为二进制码11010。

图17.18 格雷码10111转化为二进制码11010的原理
例17.19:编写8位二进制码转格雷码的转换程序。


图17.19是该程序综合的结果。

图17.19 8位二进制码转格雷码综合的结果
例17.20:编写8位格雷码转二进制码的转换程序。


图17.20是该程序综合的结果。

图17.20 8位格雷码转二进制码综合的结果
例17.21:设计一个格雷码计数器。
格雷码计数器的结构主要包括三个模块,格雷码转二进制、加法器、二进制转格雷码。首先调用格雷码转二进制模块,将格雷码转换为二进制;然后将值输出到加法器进行加法运算;之后将加法运算结果通过二进制转格雷码转换为格雷码;最后将格雷码送到输出。


下面这幅图17.21是Synplify综合以后的结果。结构非常的清晰。

图17.21 格雷码计数器综合的电路
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




