对于绝大多数的数字电路系统来说,除非它的功能非常有限,就是简简单单的一个组合逻辑,其余绝大多数能往复循环工作的电路系统都工作在一些有限个数的状态下。我们把这样一种工作方式的电路系统叫作有限状态机(Finite-State Machine,FSM)。对于这样的电路系统来说,系统实际是在有限个状态之间进行转移和运行。进行这样的系统开发的时候,用有限状态机的方法来进行硬件语言描述,结构非常简单、清晰和明了。这一章我们就来研究一下有限状态机。
比如说对于一个红绿交通灯系统来说,它的运行就是在红、绿、黄三个状态之间来回转换。为了简化问题,我们暂时忽略了空闲、故障这些状态。
在当前状态是红灯的时候,系统会显示红灯,同时进行计数。比如说红灯保持60秒,一秒记一个数,那就一直计数从0计数到59。没到59的时候,下一个状态还设置为红灯。计数器判断到59了,红灯要结束了,绿灯要开始了,下一个数就要归0,同时把下一个状态设置为绿灯。
到下一个时钟边沿触发来的时候,绿灯状态赋值给当前状态。同时开始计数,从0开始,假设绿灯保持60秒,一秒记一个数,那就一直从0计数到59。没到59的时候,下一个状态还设置为绿灯。计数器判断到59了,绿灯要结束了,黄灯要开始了,下一个数就要归0,同时把下一个状态设置为黄灯。
到下一个时钟边沿触发来的时候,黄灯状态赋值给当前状态。同时开始计数,从0开始,假设黄灯保持3秒,一秒记一个数,那就一直从0计数到2。没到2的时候,下一个状态还设置为黄灯。计数器判断到2了,黄灯要结束了,红灯要开始了,下一个数就要归0,同时把下一个状态设置为红灯。
由此,周而复始的,红绿黄灯循环工作。
从上面红绿交通灯这个例子我们可以看到,这样一种循环工作的电路系统,它的状态个数是有限的,当前所在的每一个状态下做的事也是重复的,根据信号达到什么条件进而下一个时刻状态进行变更也是明确的。
实际上这个例子就是(同步)有限状态机。后面,我们在提到有限状态机的时候,默认它就是同步的。
看图11.1,是Mealy状态机的工作示意图。
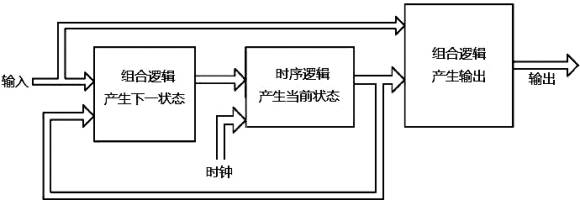
图11.1 Mealy状态机的工作示意图
我们还是以红绿灯系统对上图进行介绍。可以看到,这个系统实际上有3大块的内容:
(1)产生下一状态的组合逻辑。图中的左边部分。这一部分电路是组合逻辑电路,它的作用是用来产生下一个状态。那么,它是根据什么来产生下一个状态的呢?它有两个输入:一个是当前状态,一个是外界的输入。比如当前处在红灯,那么下一个状态可能是绿灯,可能不是绿灯(如果计时没到59的话),但绝不是黄灯。当前红灯状态下计数器的计数值到59了,则下一个状态就是绿灯,没到59下一个状态依然保持红灯。也就是说,计数会影响到第一个组合逻辑(影响的方式是计数结果被作为最左边组合逻辑的输入)。
在红绿灯这个例子里,最左边的第一个组合逻辑不需要外界输入。有很多例子是需要外界输入的。比如家居看护机器人的电路系统。机器人每天重复要做的事就是端茶、送水、按开关等重复动作,这些动作需要有外部的输入,比如病患的语音信号等等。
(2)产生当前状态的时序逻辑。图中的中间部分。这一部分电路是时序逻辑电路,它的作用是用来产生当前状态。在时钟的边沿触发下,这个时序逻辑电路开始工作。
(3)产生输出的组合逻辑。图中的右边部分。这一部分电路是组合逻辑电路,它的作用是用来产生输出。比如,每个灯保持时间的计时,是不是得把当前计时了多少秒显示在显示屏上好让司机能知道?这部分组合逻辑电路就是起这个作用的。
同时,最右边的组合逻辑电路还需要外部的输入。在红绿灯这个例子我们暂时还看不到。
实际上还有另外一种有限状态机,它是Moore状态机。如图11.2所示。
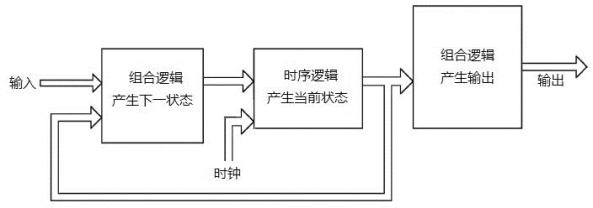
图11.2 Moore状态机示意图
其实可以把Moore状态机看作是Mealy状态机的子集。Moore状态机的输出不需要外界的输入信号。比如红绿灯这个例子,它某些方面看起来更像是一个Moore状态机。
例11.1:用有限状态机设计一个模3计数器。
模3计数器指的就是这个计数器从00开始计数,01,10,又回到00。每计数3次就是一个循环。

图11.3是综合以后的RTL视图。
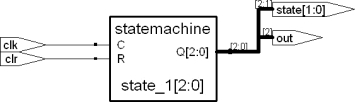
图11.3 模3计数器RTL综合结果
可以看到左边是输入,中间是状态机,右边是输出,非常简洁清晰的结构。
图11.4是综合以后的技术视图,相当于是把上图更加细化,能看清楚一些细节。很明显,上图的有限状态机用到了D触发器、或非门等结构。
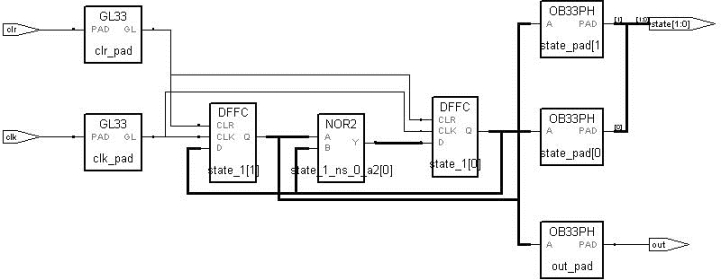
图11.4 模3计数器综合的技术视图
例11.2:用有限状态机的思想设计一个3位的二进制加1计数器。
3位的二进制加1计数器从000加到111,一共有8种可能性。这是个8状态循环的状态机。

例11.3:设计一个3位的左循环一个1的环形计数器。
3位的左循环一个1,那么状态分别应该是001、010、100的往复循环。我们可以用有限状态机来实现它。
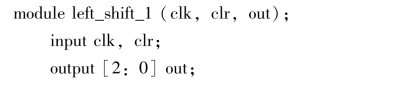

例11.4:设计一个3位的右循环一个0的环形计数器。
3位的右循环一个0,那么状态分别应该是110、011、101的往复循环。用有限状态机来实现它。

例11.5:设计一个“1010”串行数据序列检测器。要求是:当串行输入数据in中出现“1010”时,输出out为1,其他输入in情况下输出out为0。
这是一个串行的数据输入序列,我们要从高位到低位依次检测到“1”、“0”、“1”和“0”。对于输入的数据in,一个位宽,in的可能性要么是“1”,要么是“0”。电路在当前的状态下,就得有2个分叉:接到“1”时转入一个状态,接到“0”时转入另一个状态。
1,假设系统的初态是任意态,定义为S_arb,此态下:若下一个in是“1”,则系统进入到可能检测到“1010”序列最左边第一个“1”的状态,设置下一状态为S_1,同时out=0,进入第2步;若下一个in是“0”,则系统没有可能进入到检测到“1010”序列最左边“1”的状态,设置下一状态为S_arb,同时out=0,回到第1步;
2,假设系统当前处于状态S_1,要想检测到“1010”序列,我们希望下一个in信号是“0”。在S_1此态下:若下一个in是“1”,则之前的检测无效,系统默认检测到的是“1010”序列第一个“1”的状态,设置下一状态为S_1,同时out=0,进入第2步;若下一个in是“0”,则系统认为检测到了“1010”序列左边第2位“0”了,设置下一状态为S_10,同时out=0,进入第3步;
3,假设系统当前处于状态S_10,要想检测到“1010”序列,我们希望下一个in信号是“1”。在S_10此态下:若下一个in是“0”,则之前检测无效,系统设置下一状态为S_arb,同时out=0,进入第1步,重新开始;若下一个in是“1”,则系统默认检测到的是“1010”序列左边第3位“1”的状态,设置下一状态为S_101,同时out=0,进入第4步;
4,假设系统当前处于状态S_101,要想检测到“1010”序列,我们希望下一个in信号是“0”。在S_101此态下:若下一个in是“1”,则之前检测被打断,系统默认检测到的是“1010”序列左边第1位“1”的状态,设置下一状态为S_1,进入第2步,同时out=0;若下一个in是“0”,则系统已经接收到了“1010”序列,设置下一状态为S_1010,输出out=1,进入第5步;(https://www.xing528.com)
5,假设系统当前处于状态S_1010,在S_1010此态下:若下一个in是“1”,则系统默认开启新一轮检测,此时检测到的是“1010”序列左边第1位“1”的状态,设置下一状态为S_1,进入第2步,同时out=0;若下一个in是“0”,则系统设置下一状态为S_arb,输出out=0,进入第1步;
本例子假设检测不可重,也就是检测到序列“1010后”,开始新的检测时,不会把上一次检测到的序列“1010”的右边2位“10”视作新的检测状态S_10。


图11.5是Synplify综合后的结果。
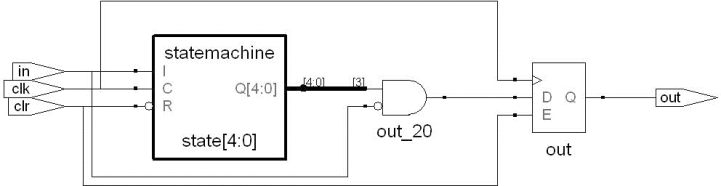
图11.5 “1010”串行数据序列检测器Synplify综合结果
如图11.6所示,右键单击statemachine,在弹出的菜单里点击View FSM。
图11.6 观察“1010”串行数据序列检测器的FSM
图11.7是它的状态转移图(输入和输出的部分需要自己添加)。
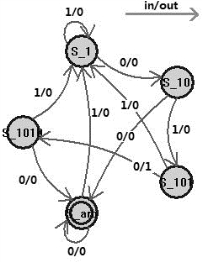
图11.7 “1010”串行数据序列检测器的状态转移图
状态转移图是描述有限状态机的工作流程的最好的方式。圆圈里的是状态,箭头指向下一个状态。图片右上角箭头符号上面的in/out表示输入in时,输出out,同时按照箭头指向转移到下一个状态。比如图中的当前状态S_arb,in=0时,输出out=0,同时下一个状态依然转移到S_arb;当前状态S_arb,输入in=1时,输出out=0,同时下一个状态转移到S_1。
在很多别的参考资料里,Moore型和Mealy型有限状态机的状态转移图格式都不一样。别的资料里,Moore型的状态转移图的圆圈里不仅标注状态,而且标注输出,同时箭头上只标注输入。
由于我们在本章前面的内容提到过,Moore型实际上是Mealy型的一个子集。因此,在本书我们做一个新的规定:所有的有限状态机,不管是Moore型还是Mealy型,一律在圆圈里只标注状态,转移箭头符号上采用“/”的形式,“/”之前是输入,“/”之后是输出。如果没有输入,则斜杠前空白;如果没有输出,则斜杠后空白。
例11.6:设计一个基于有限状态机的自动售货机。很多商场都有自动售货机,售卖各种布娃娃,一个20元,有两个投币口,顾客可以在5元投币口连续4次投币,共投入20元,或在10元投币口投2次,每次10元,或者先投入1次5元,再投入10元和5元,等等。不找零。可以设计一个in[1:0]的信号,in[0]为5元投币孔信号,in[0]=1表示投币5元,in[0]=0表示投币0元;in[1]为10元投币孔信号,in[1]=1表示投币10元,in[1]=0表示投币0元。可以设计一个out的信号表示是否已收到20元可以提供货物。可以定义四个状态:S0表示初始的状态、未投币、已提供货物;S1表示已投币5元;S2表示已投币10元;S3表示已投币15元。


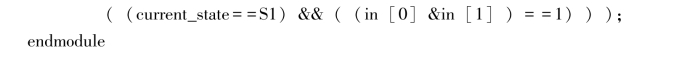
图11.8是综合以后的结果。
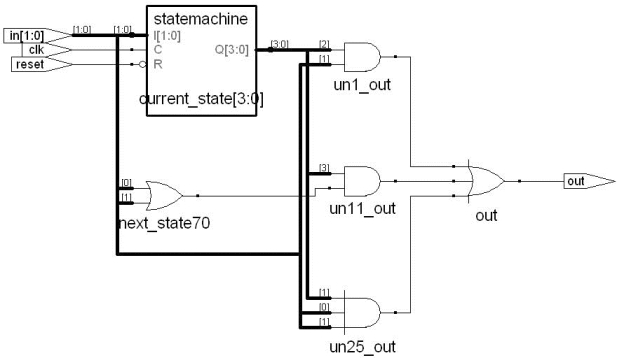
图11.8 自动售货机的综合结果
例11.7:从一个串行输入信号中探测出100110序列。


图11.9是仿真的结果。

图11.9 “100110”序列探测的仿真结果
上面这个例子,如果是仅仅作为电路来说,状态信号state是没必要设置为输出的。但是为了在仿真器观察它的变化,我们给state信号设置为输出。
in是随机设置的串行输入信号。在图中圆圈区域,in出现了连续的100110序列。相应的state状态依次出现了1-2-3-4-5-6的状态变化。探测到该序列后,out立刻显示出了一个上升沿。
请读者注意观察clk、in和state的边沿关系。每次clk上升沿来了,才会有state的变化(如果state应该有变化的话)。这就是时序触发电路的特性。
请读者仔细观察圆圈区域out的上升沿时刻、状态6出现的时刻、相对应的clk上升沿时刻。如果放大了看,这三者的先后关系为:先有clk上升沿,经过上升沿触发所需要的细微的延时,状态出现got100110(也就是状态6),立刻执行组合逻辑电路(执行过程意味着电流流过一段长度的电路,有了一定的电路延时),生成out上升沿。出现out的上升沿,是由assign语句执行综合得到的。我们看源代码倒数第二句assign语句,状态一旦变化为got100110(也就是状态6)那一瞬间,就会给out赋值为1,除了适当的器件延时,这种赋值不需要等待。这就是组合逻辑电路的特性。
例11.8:下面是一段简单的有限状态机的描述,请读者试着在纸上描绘出它的状态转移图。

![]()
例11.9:下面这个例子是一个有3个阶段流水线操作的例子。

图11.10是其综合的RTL视图。三级流水线的特征很明显,每一级都有运算操作和D触发器。

图11.10 3个阶段流水线操作的综合结果
这个例子长得和之前我们见过的例子很不一样。之前我们学到的有限状态机都是具有case的分支选择结构,case语句根据信号或状态的变化来寻找分支,分支里会计算相应的输出和状态变化。而这个例子呢,完全见不到case语句结构的身影。我们在这个例子里用了3个always语句块,每个语句块进行相应的计算,产生相应的输出。因为这个例子综合的结果是一个3级流水线的结构,我们可以把每一级的输出看作是一个状态的响应(包括该状态时的输出和下一状态的确定)。只不过,这个例子里没有明确的写出这3个state。因此,我们可以认为这个例子的描述方法是一种隐式状态机。
延伸一下,假如这是个更多级的流水线结构呢?假如某级输出寄存器反馈回另一级进行计算呢?实际上,延伸出来的这两点恰恰就是我们之前见过的显式状态机的基本特征。显式状态机具有的一个结构特征就是状态之间不一定是一个方向的循环,中途可能会从一个状态直接跳到另一个状态而不走单方向循环。显式状态机具有的另一个结构特征就是每个状态的输出都是根据各种输入来计算的,这些输入的来源可以来自各个状态。
读者要尝试着学会这种隐式的有限状态机的基本写法。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




