组合逻辑电路设计思路

按照是否有时序触发的功能来分，数字电路可以被分为2种类型，一种是组合逻辑电路，另一种是时序逻辑电路。这一章，我们重点学习组合逻辑电路的基本设计思路。组合逻辑电路的意思就是说，这种电路你把它做好之后，一旦输入端有信号输入进来，电路就会立刻计算并输出，没有任何节奏。

例9.1：设计一个半加器。

半加器可以实现两个一位的二进制数的加法，输出包括一位的和，同时还有一位向上的进位位。

这个例子里，我们定义了寄存器sum和cout，因为它们要在always块里被赋值。我们使用了case语句，使用了拼接运算符，大大简化了源代码。

利用半加器，我们可以实现1位二进制数加1位二进制数的运算结果。有些时候，我们可能遇到多位二进制数相加且有进位位输入的情况，这时候就需要用到全加器。

例9.2：设计一个有低位进位位输入、能实现2个1位二进制数相加的全加器。

我们也可以把上面这个例子修改一下，让它变成可以实现更多位二进制加法的全加器。

例9.3：设计一个3-8译码器。

一般来说，译码器指的是从一种数据表示形式转换为另一种数据表示形式的器件。比如3-8译码器，输入端有3条数据线（总共有从000～111共8种可能性），要把它表示的信息转换为（输出端）8条数据线的形式。这就叫作译码。

例9.4：组合逻辑电路。

这个例子把alpha和beta做异或，其结果再与gamma相与。请读者把这个例子以原理图输入的方式在ISE生成该程序，并做仿真。

例9.5：组合逻辑电路。

这个例子对5位输入alpha和beta的大小进行比较，如果alpha小于beta，则把alpha的值赋值给输出；否则，把beta的值赋值给输出。读者看到这个例子的时候，可以想象一下，这样的例子，综合器会综合出一个什么样的电路。图9.1是Synplify综合的RTL电路视图。

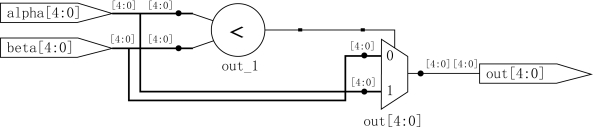
图9.1　组合逻辑电路实例综合结果

其中，在Synplify软件打开小于号代表的电路结构，会发现该部分结构很复杂。小于号比较的结果作为一个二选一多路选择器的选择端。

例9.6：组合逻辑电路。

这是一个高考招生的例子，alpha和beta是输入的两个人的成绩，fen_shu_xian是分数线。先判断alpha大于分数线吗？大于分数线，则把alpha留下继续比较。再判断beta大于分数线吗？大于分数线，则把beta留下继续比较。小于分数线，则留下的都是分数线。最后比较alpha＜beta，根据前两次比较的结果，决定是输出alpha，还是beta，抑或是分数线。若输出分数线，很明显，则alpha和beta都未通过。

例9.7：组合逻辑电路。

sel=0，则把alpha*beta的值赋值给输出；否则把gamma*delta的值赋值给输出。

把上面这个例子改写一下。

例9.8：组合逻辑电路。

例9.9：以下是BCD码、余3码、独热码等几种编码方式的基本原理，读者试着编写它们之间的转换电路。

BCD码指的是二进码的十进数，也叫作二-十进制代码（Binary-Coded Decimal）。它是用4位二进制数来表示1位十进制数中的0～9这10个数码。可以把它看作是二进制编码的十进制代码。由于十进制数共有0、1、2……9十个数码，因此，至少需要4位二进制码来表示1位十进制数（2的4次方等于16）。把BCD码加3，就可以得到余3码。也就是把二进制的BCD码加二进制的“0011”，就可以得到对应的余3码。

余3码的特点就是，当两个十进制数的和是10的时候，相应的二进制编码正好是16（想想为什么是16？因为每个BCD码都加3，BCD码的和10，10+3+3，就是16）。于是余3码可自动产生进位信号，而不需要进行修正。BCD码的和为10的对应的余3码可自动产生进位信号，那BCD码的和为9的呢？这就意味着0和9、1和8、2和7、3和6、4和5的余3码互为反码，这在求对于10的补码很方便。

独热码，其英文为one-hotcode，简而言之就是有多少个状态就有多少比特，每一个状态有且只有一个比特为1，其他全为0的一种编码方式。举个例子，有8个状态的独热码状态编码为：0000_0001，0000_0010，0000_0100，0000_1000，0001_0000，0010_0000，0100_0000，1000_0000。其中下划线是为了阅读的方便而添加，不影响编译。再比如，有十六个状态的独热码状态编码应该是：0000_0000_0000_0001，0000_0000_0000_0010，0000_0000_0000_0100，0000_0000_0000_1000，0000_0000_0001_0000，0000_0000_0010_0000，……，1000_0000_0000_0000。一般来说，为了书写的便利，将二进制简化为用十六进制来表示（从右边最低位往左边每四位二进制位用一位十六进制数表示），那么，以上十六状态的独热码可以表示成0x0001，0x0002，0x0004，0x0008，0x0010，0x0020，……，0x8000。独热码编码消耗的逻辑单元较多。但是，独热码编码有个最大优势就是：在判断状态的时候只需要比较一个位，这就从很大程度上简化了译码逻辑电路。同时，在一些比如有限状态机的转换的时候，状态与状态之间的转换，实际可以以移位寄存器的方式来实现。这对于减少一些电路噪声，有很大的好处。编码消耗的电路逻辑多，而译码消耗的电路逻辑少，这就是独热码。

例9.10：设计一个数据分配器。

假设有一个器件，输入端是一位二进制数的输入端in，有2个输出端out1和out2，根据需要，随时把输入信号发送到任意一个输出端。这就还需要一个起选择哪个输出端的控制作用的输入端。这个选择端只要1个二进制位就行，1个位就具有2种可能性，可以在两个输出端中二选一。

数据分配器的真值表如下表所示。

表9.1　数据分配器的真值表

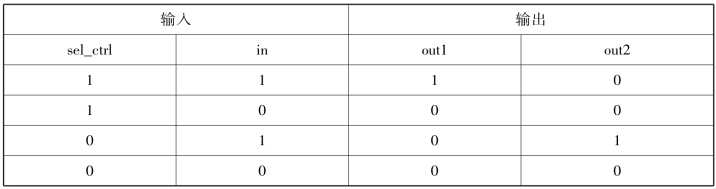
其中，sel_ctrl为1时，把in的信号传送给out1，in是多少，out1就赋值为多少，此时，out2保持0；sel_ctrl为0时，把in的信号传送给out2，in是多少，out2就赋值为多少，此时，out1保持0。

作业：对于数据分配器这个例子，试着添加一个使能信号，使得在使能信号的控制下，系统才能进行数据分配。

例9.11：设计一个三态缓冲器。

在计算机中，每一个器件要与外界沟通，就需要与外界之间相互进行数据、地址和控制信号的传输。为每一个器件单独配置它专用的传送信息的传送线是不可能的。所以，绝大多数的计算机中的信息传输线均采用总线形式。总线的意思就是，如果要传送的信息是一个类别的，就走一种类别的传输线，比如数据走数据总线，地址信息走地址总线，控制信号走控制信号总线。所以，一般来说，有三种性质的总线：数据总线、地址总线和控制总线。

每一个器件（比如寄存器和存储器）都挂在总线上。哪个器件要使用总线，经过允许，总线在一段时间就让这个器件用。在这一段时间，别的挂在总线上的器件就只是挂在总线上，暂时不使用总线。那么怎么防止挂在总线上暂时不用的器件干扰到别的器件呢？这就要求寄存器或者储存器不仅能输出0和1的电平，还能呈现出第三种状态：高阻抗状态。当一个器件呈现高阻抗状态，就好像此时它的输出是被断开了的，对别的器件或者总线无影响。也就是说，所有的寄存器和存储器可以都挂在总线上，某一时刻，那些暂时不使用总线的器件，就让它的输出呈现高阻态，剩下的要使用总线的器件，就正常使用总线。

三态门这种器件即可实现上述的功能，它除具有输入端in和输出端out之外，还有一控制端en，请看图9.2。

图9.2　三态门结构图

当控制端en=1的时候，器件把它的信号通过三态门的输入端in顺利的传送给输出，输出out=输入in。此时，总线就由这个器件驱动，这个器件传送的是什么数据，数据就会通过三态门顺利的传送到总线上，进而传送出去。

当控制端en=0的时候，三态门的输出端out呈现高阻抗的状态，三态门相当于是断开的。此时，这个器件虽然是挂在总线上，却对总线不起作用。

这么看来，三态门就是一个缓冲，在寄存器和总线之间起着缓冲的作用。

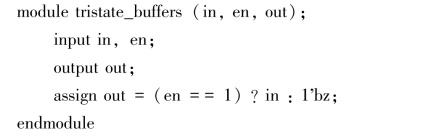
例9.12：设计2个三位二进制数的比较器。

两个二进制数，每个数都是3个位的二进制数，每个数的范围就是000～111。两个数进行比较，假设一个是alpha，一个是beta。有3个输出端口，alpha_larger、beta_larger和equal。

图9.3　三位二进制数的比较器综合结构图

如果alpha>beta，则alpha_larger=1、beta_larger=0和equal=0；

如果alpha＜beta，则alpha_larger=0、beta_larger=1和equal=0；

如果alpha=beta，则alpha_larger=0、beta_larger=0和equal=1。

例9.13：设计一个如下几种基本的二输入逻辑门电路：与、或、非、与非、或非、异或、同或。

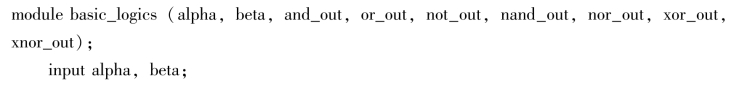
例9.14：设计一个8-3编码器。

有些时候，在电路设计的过程中，会出现存在多个逻辑输入的情况。

比如说，如果我们有8个按键，想把这8个按键接到单片机的管脚上，一个按键接单片机一个管脚，单片机根据各个管脚是否有按下来获取信息。往往会存在这种情况：单片机的可用管脚不多了，单片机没有8个管脚来一对一的连接8个按键了。怎么办？8个按键就得有8个单片机的管脚来对应，要是有16个按键，单片机是不是得留出16个管脚来对应？肯定不行。

所以，我们可以考虑设计一个编码器，8个按键（8根线）连接在编码器的输入端，编码器有3个输出端（或者说输出的是3根线），3个2进制的输出端接到单片机的3个管脚。这就降低了对单片机的管脚资源需求。3个输出端一共有2的3次方等于8种输出的可能性。

当按下某一个按键时，编码器就会产生相应的编码信号，单片机会接收到这个编码值，进而分析出是按下了哪一个按键。

这就是8-3编码器。下面我们来设计一个8-3编码器。

for循环从低位开始搜索，若有多按键按下，以最后一个为1的位为准。

例9.15：设计一个无符号的3位乘法器。

下图是综合以后的结果。

图9.4　无符号的3位乘法器综合结果

例9.16：设计一个带使能功能的2-4译码器（门级）。

下图是它的综合电路。(www.xing528.com)

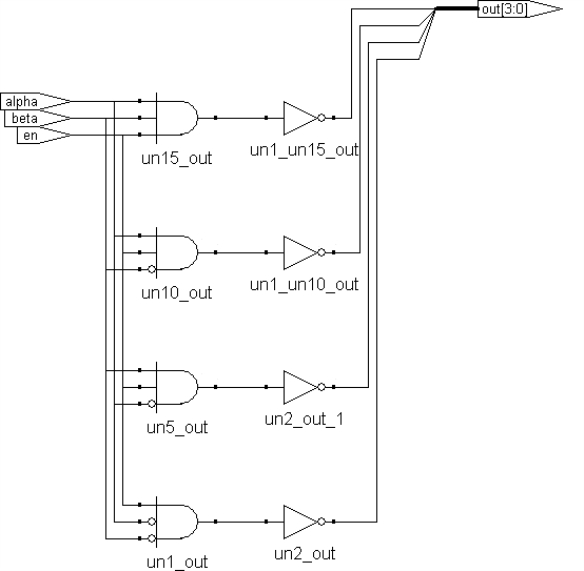
图9.5　带使能功能的2-4译码器门级综合结果

像上面这个例子，它使用了assign语句。通过assign连续赋值语句，我们可以给wire类型的变量赋值。对于assign#2nalpha=～alpha这条语句，只要右边的表达式（有时候alpha可能很复杂，是个复杂的表达式）有变化，就立刻重新计算右边表达式的值。经过了#2时间单位的延迟后，赋值给左边nalpha。

上面这种代码的描述风格就叫作数据流风格的描述。它的特点就是使用assign连续赋值语句。

上面这个例子，我们使用了6个连续赋值语句。要指出的是，这些赋值语句是并发执行的。什么叫作并发执行？并发执行的意思就是说这6条语句的执行顺序是同时执行的，把哪一条语句写在前、哪一条语句写在后，都不影响结果。

例9.17：设计一个带使能功能的2-4译码器（门级实例调用）。

这也是2-4译码器的例子，使用的是门级的实例调用。综合的电路和前面的那个例子一模一样。

例9.18：设计一个全加器。

前面的例子里，我们设计了半加器、全加器。半加器的输入不需要有低位的进位位。全加器的输入需要有低位的进位位。这就是它们的区别。

在之前的例子里，我们设计的全加器使用了assign连续赋值语句。我们接下来再看一个全加器的例子，使用always语句。

图9.6是综合以后的结果。

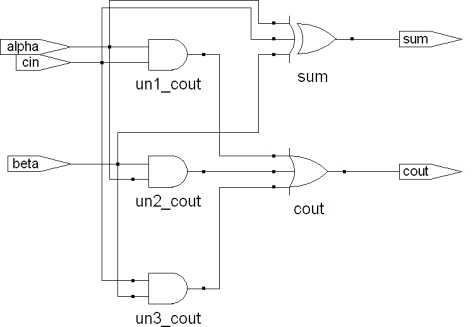
图9.6　全加器综合结果

always语句里使用了begin-end顺序块。顺序块的意思是：begin-end里的语句按照顺序执行。begin-end顺序块里的语句是过程性赋值语句。过程赋值语句分两种：阻塞过程赋值语句（用“=”赋值）的意思是得等前一条语句执行完了才轮到下一条语句执行；非阻塞过程赋值语句（用“＜=”赋值）的意思是前一条语句和下一条语句同时执行。

过程性赋值语句可以带有延迟。

有两种类型的延迟：一种是语句间的延迟，指的是语句与语句之间的延迟，也就是在执行本条语句之前需要等待的时间；一种是语句内的延迟，指的是一条语句之内的延迟，也就是这条语句计算出了右边的值后需要等待一定的时间后才赋值给左边，比如之前的例子“assign#2nalpha=～alpha”，就是语句内延迟。

本例中，如下两句代码，第二行的#2就是语句间的延迟。

第一条语句执行完了之后，需要等待2个时间单位，才开始执行第二条语句。

这个例子中，我们使用了always语句，always语句总是在不断地往复循环执行中，这种描述的方法就是行为风格的描述。

除了always语句之外，还有一种行为风格的描述方法，就是使用initial语句。initial语句只执行一次。下面我们看一个initial语句。

上面这个顺序块从0时刻开始执行，从语句1执行到语句6，只执行1次。

第0ns，语句1执行。alpha被赋值为0。语句1是阻塞赋值。没有延时，语句2在第0ns开始执行，beta被赋值为0。

第0ns，语句3开始执行。由于语句3是语句内延时，延时2ns。第2ns时，alpha被赋值为1。语句3是阻塞赋值，得等到语句3执行完了才执行语句4。

第2ns，语句4开始执行，延时3ns。第5ns，语句4开始赋值，beta被赋值为1。

第5ns，语句5开始执行，延时4ns。第9ns，alpha被赋值为0。

第9ns，语句6开始执行，延时5ns。第14ns，beta被赋值为0。

以上就是行为风格的描述，主要使用了always和initial语句。

例9.19：使用case语句的全加器。

例9.20：使用结构描述方式和行为描述方式混合编程的组合逻辑电路。

语句1和语句2都是实例调用，实例调用了库里的逻辑门。这些门就叫作结构化组件。所以语句1和语句2是结构描述方式。

语句3使用了连续赋值语句assign。语句3是行为描述方式。

上面这段程序就是两种不同的描述方式的混合。

下图是综合以后的电路。

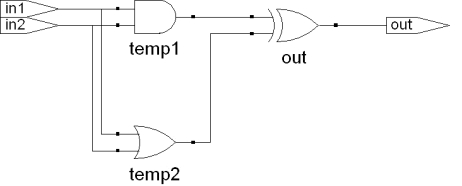
图9.7　混合编程的组合逻辑电路综合结果

例9.21：设计一个可以实现简单加、减、乘、与、或等简单功能的科学计算器电路。

假设时光回到了20世纪的40年代末期。那个时候汇编语言还没有诞生。而读者你呢，刚好作为国防部的一个工程师，参与了一个冷战的项目，目的是要发明一种语言，姑且就把它叫作汇编语言吧。那时候你通过开发这种语言，能把简单的算术逻辑运算用一行一行语言的形式表示出来，而且机器能读懂这种语言。比如说，有如下几行代码：

对于前3行代码，你首先赋值in1为4，in2为2，第三行代码的意思是：jia表示加，in1加in2的值，赋值给out。要记住你是处在20世纪40年代的科技水平和思想观念。怎么实现这个加法呢？

你做了如下设计：

（1）用了一种纸片。一行有12个孔的位置可以打孔（也可以不打）。打孔（黑色）表示0，不打孔（白色）表示1；

（2）1-3孔表示指令（或者叫作操作码），4-6孔表示输出，7-9孔表示第一个输入值，10-12孔表示第二个输入值；

（3）你事先把1-3孔状态定义如下：“000”为加法，“001”为减法，“010”为或运算，“011”为与运算，“100”为对第一个输入取反，“111”表示这一行是赋值语句；

（4）机器有个可以向下压纸片的弹出缩回的机构。这个机构后面连着一个开关，开关连着两个电平：接地“0”和5伏“1”。机器每探测完一个孔，就向右移到下一个孔的位置；

（5）1-3孔由第一个机器来探测，4-6孔由第2个机器（输出端的机器）来打孔，7-9孔由第3个机器来探测，10-12孔由第4个机器来探测。

你手动的在纸片上打孔（打孔就是写代码），形成了第一行代码，它的打孔结果如下图：

图9.8　打孔结果示意图

前三个孔为白色，表示没打孔，为“111”，表示此行赋值。机器弹缩机构依次探测每一个位，然后右移到下一个孔。到第3个机器工作时，机器读到第7孔，弹缩机构压不下去，机构后面连着的滑片连接的位置刚好连到高电平。机器读到8孔时，弹缩机构压下去了（因为此处有孔），机构后面连着的滑片连接的位置刚好连到低电平。9孔也类似。in1信号刚好接到这三个线上，于是in1赋值为“100”，即in1=4。

第二行代码，它的打孔结果如图9.9：

图9.9　打孔结果示意图

10-12孔为“010”，于是in2赋值为“010”，即in2=2。

第三行代码，它的打孔结果如图9.10：

图9.10　打孔结果示意图

图9.11　科学计算器RTL综合结果

1-3孔为000，表示这是加法，4-6孔留给输出端的机器2根据电路执行结果，由输出端的机器来打。7-9孔为“100”。10-12孔为“010”。

现在开始要设计一个电路，这个电路从外观看，是一个黑盒子。它有3个输入端，一个输出端，就如图9.11所示一样。

它的功能很简单，就是in1是一个3位的2进制输入信号，in2也是一个3位的2进制输入信号。in1连接到第3个机器后面，由第3个机器给出。机器读到第一行代码，给in1端口赋值为4。

in2连接到第4个机器后面，由第4个机器给出。机器读到第二行代码，给in2端口赋值为2。

opcode是一个3位的输入信号。纸片的前三个孔就表示opcode。opcode连接到第1个机器后面，由第1个机器给出。

这个黑盒子里面放着并行的几种组合逻辑电路：加法、减法、或、与、取反。比如说对于第三行代码，第一个机器现在探测到000，就是加法，于是机器后连接的转轮刚好滑动到连接上了加法电路。其他电路悬空。于是输入in1和in2的信号经过加法电路，计算出结果，控制第2个机器把纸片的第3行的4-6孔打出了结果4+2=6，如下图所示：

图9.12　机器自动打孔结果

下面我们编写这个黑盒子的加减或与反电路。

综合以后的结果就如图9.13所示：

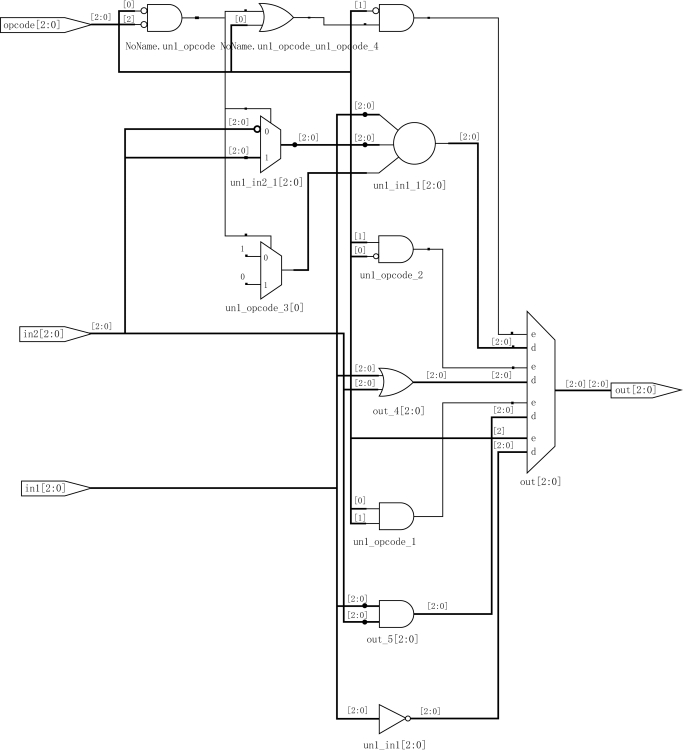
图9.13　综合结果

到此为止，你基本实现开发了一种纸片信号I/O器（包括机械和电路），发明了一种长得像现代汇编语言的语言。如果时间真的能够穿越到20世纪40年代，这会是非常伟大的两项发明。能够比肩第一代电子计算机和C语言的发明。当然，细节上还有很多要完善的地方。

可惜，这只是我们的想象。毕竟在那个年代，还没有硬件描述语言（以及计算机）可以让你如此轻松地实现一个电路的开发。

可是我们还是希望，你能从上面这个例子里，学会并掌握用一种语言搭配相应的机械电路结构来实现一个想法的基本思路。