ANSYSWorkbench17.0有限元分析：子模型概述

子模型是获得模型部分区域中更加精确解的有限元技术。在有限元分析中往往出现这种情况：对于用户关心的区域，如应力集中区域，网格太疏不能得到满意的结果，而对于这些区域之外的部分，网格密度已经足够了，如图21-1a所示。要得到这些区域的较精确的解，可以采取两种办法：

1）用较细的网格重新划分并分析整个模型。

2）只在关心的区域细化网格并对其进行分析，如图21-1b所示。

显然，前一个方法太耗费资源，后一个方法即为子模型技术，更有优势。

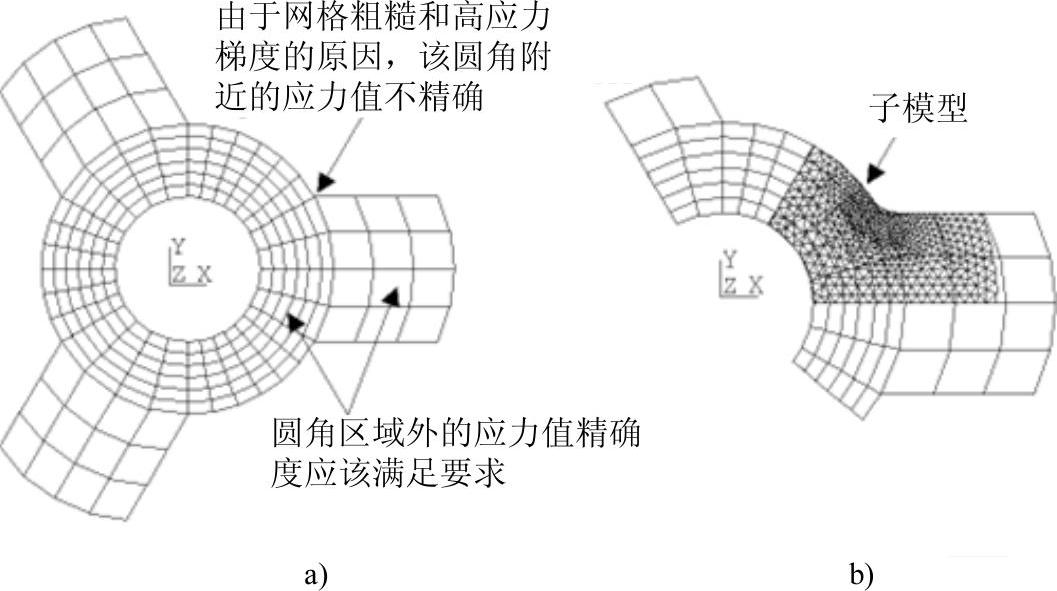
图21-1 轮毂和轮辐的子模型

a）粗糙模型 b）叠加的子模型

子模型方法又称为切割边界位移法或特定边界位移法。切割边界就是子模型从整个较粗糙的模型分割开的边界，整体模型切割边界的计算位移值即为子模型的边界条件。

子模型基于圣维南原理，即如果实际分布载荷被等效载荷代替以后，应力和应变只在载荷施加的位置附近有改变。这说明只有在载荷集中位置才有应力集中效应，如果子模型的位置远离应力集中位置，则子模型内就可以得到较精确的结果。(www.xing528.com)

ANSYS Workbench程序并不限制子模型分析必须为结构（应力）分析。子模型也可以有效地应用于其他分析中，如在电磁分析中，可以使用子模型计算感兴趣区域的电磁力。

除了能求得模型某部分的精确解以外，子模型技术还有如下优点：

1）减少甚至取消了有限元实体模型中所需的复杂的传递区域。

2）使得用户可以在感兴趣的区域就不同的设计（如不同的圆角半径）进行分析。

3）帮助用户证明网格划分是否足够细。

使用子模型的一些限制如下。

1）子模型只对3D分析有效。

2）子模型的原理要求切割边界应远离应力集中区域。