ANSYSWorkbench17.0装置分析求解：入门到精通

本节的主要内容包括：分析求解通用设置和载荷步设置。相关的内容如下所述。

1.通用设置

对于在Mechanical中进行的分析而言，大部分的通用设置将会根据选择的分析类型自动提供。这些选项位于树结构图中Analysis Settings对象下。下面对一些常用的设置进行基本的介绍。

（1）载荷步控制 载荷步控制在分析中充当着非常重要的角色。载荷步控制包括两个功能：

1）定义载荷步。

2）设置每个载荷步的分析设置参数。

关于载荷步控制的具体内容将在后文中讲述。

（2）求解器控制 求解器控制的内容根据分析的类型改变，不同分析类型条件下求解器控制的属性情况见表5-11。

表5-11 求解器控制属性

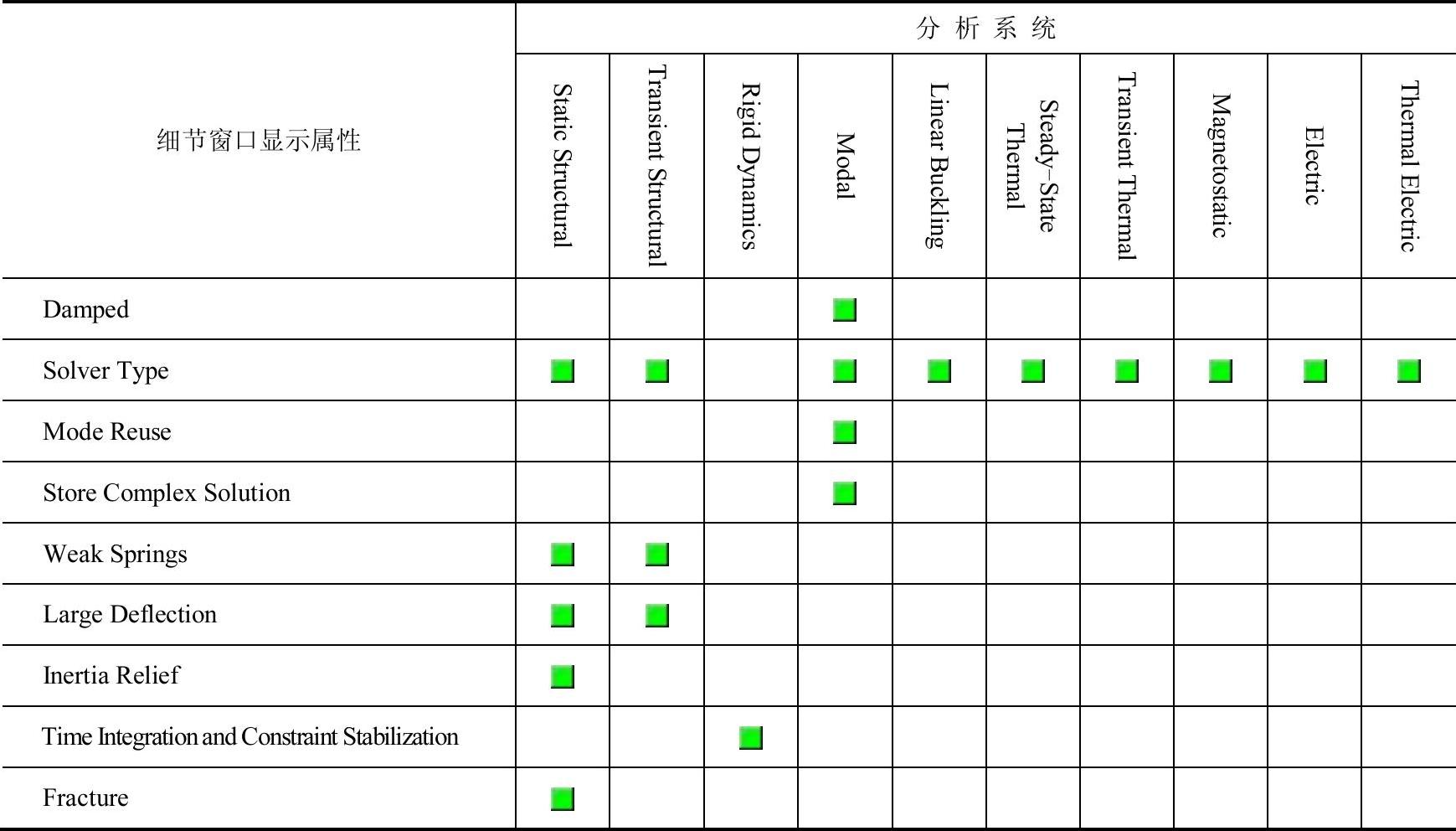
注：为显示属性。

（3）重启分析 在静力结构分析和瞬态结构分析中可以使用重启分析（Restart Analysis）来获得从某时刻重新启动分析所需的数据库。

（4）蠕变控制 在静力结构分析和瞬态结构分析中可以使用蠕变控制来对材料的蠕变效应进行考虑。这在模型承载时间非常长的分析中有必要使用。

（5）循环控制 可以设置循环对称结构在模态分析中获取求解结果的方式。

（6）辐射控制 辐射控制可以在热相关分析中考虑辐射的因素进行控制。

（7）分析相关选项 分析相关选项根据分析的不同而不同。例如，在进行模态分析的时候，设置的求解方法可以为模态叠加法和完全法等。

（8）阻尼控制 在进行动力学分析时，可以设置阻尼。

2.载荷步控制

加载过程中，载荷步、子步和平衡迭代是控制加载求解过程的重要手段，而这些均以ANSYS Workbench定义的时间和加载方式为基础。

（1）载荷步、子步和平衡迭代 载荷步、子步和平衡迭代是控制加载求解过程的3个载荷时间历程节点。

1）载荷步。载荷步（Step）是可以获取正确求解结果的、由用户直接定义的加载配置的载荷设置间隔，是用户分次输入载荷的结果。

■在线性静态分析或稳态分析中，可以使用不同的载荷步施加不同的载荷组合。例如，在第一个载荷步中施加惯性载荷，在第二个载荷步中施加力载荷，在第三个载荷步中施加力和惯性载荷以及一个不同的位移条件等。图5-51a所示为在不同载荷步施加不同载荷的情况。

■在瞬态分析中，可以将多个载荷步加到同一加载历程曲线的不同时间点。图5-51b所示为一个需要3个载荷步的载荷历程曲线：第一个载荷步用于加载渐变载荷，第二个载荷步用于加载不变载荷，第三个载荷步用于卸载。在每个载荷步的终点，载荷值均达到用户指定的值。

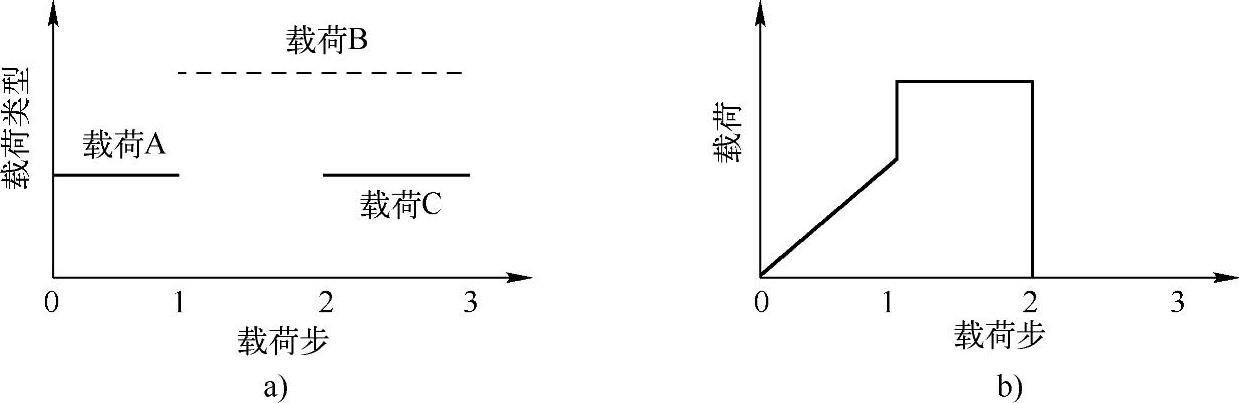
图5-51 载荷步加载过程

a）稳态分析加载步骤 b）瞬态分析加载步骤

2）子步。子步（subStep）是载荷步中载荷逐渐施加到有限元模型上的过程中进行求解的点。图5-52所示为瞬态分析加载过程中的载荷步和子步之间的关系。从图中可以看到，在第一个载荷步中，载荷被分成了3个子步逐步计算；在第二个载荷步中也是如此；在第三个载荷步中，使用两个子步完成了卸载。(www.xing528.com)

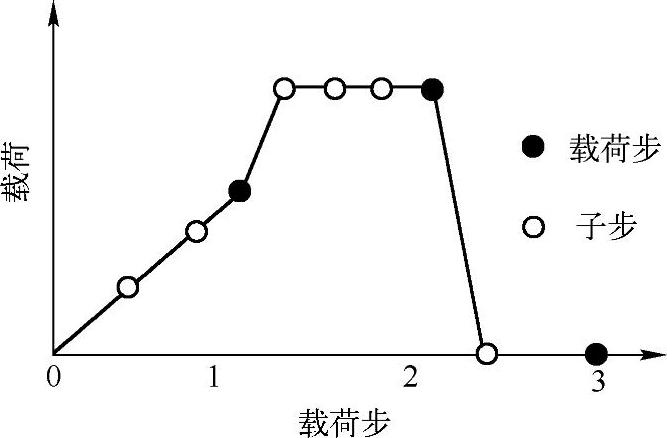
图5-52 载荷步下的子步

子步对求解过程的控制非常重要，很多时候需要使用不同的子步数来满足不同的加载和求解需要：

■在非线性静态和稳态分析中，使用子步逐渐施加载荷以便能提高求解精确度，甚至使求解结果从不收敛转化为收敛。

■在线性或非线性瞬态分析中，使用子步满足时间步长的需要，得到较为精确的解，即满足瞬态时间累积法则。

■在谐响应分析中，使用子步获得谐响应频率范围内多个频率处的解。

3）平衡迭代。当子步的载荷施加到有限元模型上时，求解器开始求解子步载荷的结果。有限元常使用迭代来求解，在迭代的过程中逐渐逼近子步载荷，使用迭代方程（省略其他变量）可以表示为

f（L_n，L_n−1，L）=0

式中，L为子步载荷，L_n为第n次迭代的结果，当满足|L−L_n|<L_err时，停止迭代。L_err为残差标准。通常一个子步求解需要经过若干次迭代，每次迭代都被称为一次平衡 迭代。

（2）时间ANSYS Workbench对所有的静态和瞬态分析都使用时间作为跟踪参数，即在指定载荷历程时，在每个载荷步的结束点赋予时间值，而不论载荷类型是否依赖于时间。这样，计算的结果将是与时间有关的函数：

1）在静态线性分析中，时间取为常量0。

2）在瞬态分析中，时间作为表示真实时间历程的变量在变化。

3）在其他分析中，时间仅作为一个计算器，识别求解时所采用的不同载荷步。

另外，时间也可作为一个识别载荷步和载荷子步的跟踪器。从时间历程上讲，载荷步是作用在指定的时间间隔内的一系列载荷；子步是载荷步中的时间点，平衡迭代求取的是子步时间点上的中间解。

使用时间作为跟踪器的优势在于：在所有情况下可以使用一个不变的“跟踪器”对求解历程进行跟踪，而不需要再依赖于具体分析的特殊物理量；而时间是单调增加的，能够代表自然界中发生的现象，因为自然界发生的大多数现象都必定经历一段时间，无论这个时间是多么短暂。

在瞬态分析或率相关的静态分析（如蠕变或粘塑性分析）中，时间跟踪器能具体地代表实际的按年月顺序的时间。在指定载荷历程时，指定每个载荷步的结束点的时间值。在其他分析中，时间作为一个识别载荷步和载荷子步的计数器，是ANSYS Workbench内部变量，不再表示具体的时间值。

在后处理中，可以使用时间作为自变量，其他分析量作为因变量来查看时间历程上的结果信息。这时，时间历程上的结果是每一个子步结束时求取的结果。

（3）阶跃载荷和渐变载荷 施加载荷有两种基本方式：阶跃载荷和渐变载荷。前一种方式，载荷被突然施加到对象上；而后一种方式，载荷被缓缓地施加到对象上。

在ANSYS Workbench中，载荷步的时间终点的载荷值达到指定的值，根据施加载荷的不同，载荷达到指定值的方式也不同。根据载荷步中载荷达到指定值的时间不同，按以下两种方式定义施加方式不同的载荷：

■阶跃载荷（Stepped Load）—指定载荷施加于第一个载荷子步，且在载荷步的其余

部分载荷保持不变，如图5-53a所示。

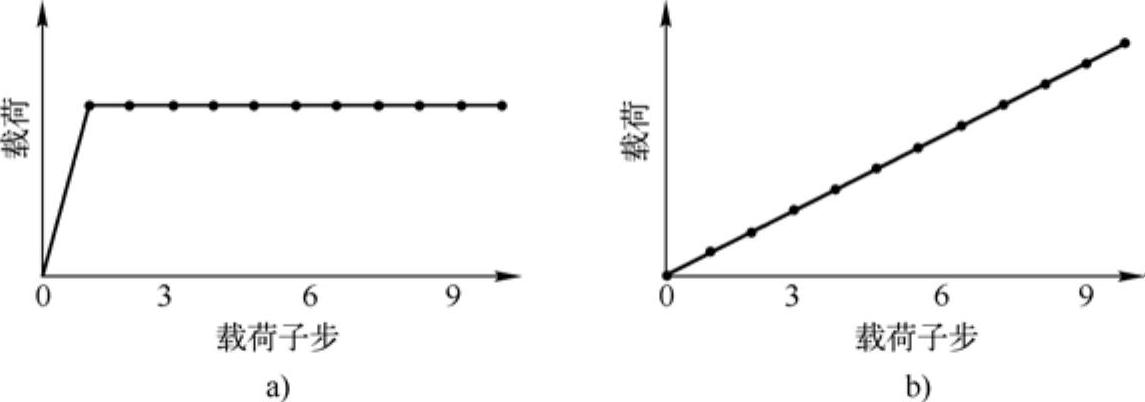
图5-53 载荷施加方式区别

a）阶跃载荷 b）渐变载荷

■渐变载荷（Ramped Load）—在每个载荷子步，载荷值逐渐增加，指定载荷出现在载荷步结束时的最后子步，如图5-53b所示。

两种载荷在ANSYS中的设置方式如下文所述。