河川径流时间序列小波变换实施效果

河川径流变化不存在真正意义上的周期性，而是时而以这种周期变化，时而以另一周期变化，并且同一时段中又包含各种时间尺度的周期变化，在时域中存在多层次时间尺度结构和局部化特征。传统的傅里叶分析不能分析出这一特征，而小波分析方法能克服这一缺点，它可以通过伸缩和平移等运算功能对函数或信号序列进行多尺度细化分析，研究不同周期随时间的演变情况。

以黄河上游兰州站，黄河中游三门峡站，黄河下游花园口站为代表，三站多年平均径流量分别为327.55亿m3、501.53亿m3 和558.52亿m3。应用小波分析理论，对黄河上、中、下游河川径流长系列进行深入细致的分析，以揭示黄河主要水文站河川径流的变化特性，使我们对黄河径流变化有更加深刻的认识，为黄河流域规划、水资源优化配置等提供更加全面的技术支持。

在进行小波变换之前，先对资料做预处理，方法如下。

首先，求径流时间序列的距平值。采用兰州站、三门峡站和花园口站1919～1997年共79年天然径流资料，求其距平值，应用距平值序列，小波分析前径流资料可以滤掉1年的自然周期。图8-8为兰州站、三门峡站和花园口站天然径流序列距平曲线。

其次，增加端点的资料。由于实际处理时数据长度总是有限的，因此在数据的起端和终端小波函数将会越出数据之外。

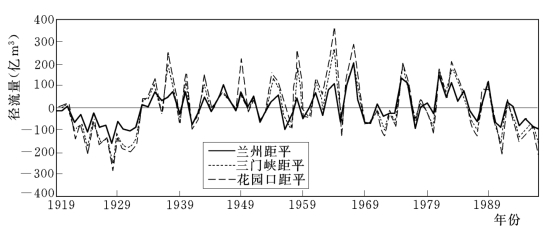
图8-8　三站径流距平曲线 （1919～1997年）

通常采用的补救方法是令数据周期循环 （设数据xn的范围n=0～N，则取x-k=xN-k，xN+k=xk），或是把数据反摺 （取x-k=xk，xN+k=xN-k）。本文采取第二种方法，即将数据反摺以增加资料长度。

设原资料序列为f（1），f（2），…，f（n）

向前延伸n点：f（-i）=f（i+1），i=0，1，2，…，n-1

向后延伸n点：f（i+n）=f（n+1-i），i=1，2，…，n

增加两端资料后，资料序列变为

当小波变换完成后，去掉两端的小波变换系数，只保留原有资料的小波系数。这种处理方法使增加的数据与原有序列具有相同的性质，使边界部分的性质不产生歪曲现象。

数据处理后，采用Morlet复值小波对三站径流序列进行连续小波变换，可以得到小波变换系数的实部、虚部、模、模平方、相位等信息，通过分析这些信息，能够揭示河川径流变化的多时间尺度结构。

8.4.9.1　黄河上游小波变换结果及分析

图8-9～图8-13分别为兰州站河川径流序列Morlet小波变换系数的实部、虚部、模、模平方、相位等值线图。

（1）小波系数实部。

小波系数的实部包含着给定时间和尺度信号相对于其他时间和尺度信号的强度和相位两方面的信息。Morlet小波的实部本身也是一个对称的小波函数，它可以看成是一个平滑函数的三阶导数。

小波系数并不是真正的径流量值，两者存在正相关关系，某一时间尺度的正小波系数与该时间尺度下径流量变化的丰水期相对应，图中用实线绘出，而负小波系数与枯水期相对应，图中用虚线绘出，正值中心对应丰水中心，用“+”表示，负值中心对应枯水中心，用 “-”表示。从小波系数的实部可以看出不同尺度下的丰枯相位结构，即不同的时间尺度所对应的径流丰枯变化是不同的。小尺度的丰枯变化则表现为嵌套在较大尺度下的较为复杂的丰枯结构。

图8-9　兰州站Morlet小波变换系数实部

图8-10　兰州站Morlet小波变换系数虚部

图8-11　兰州站Morlet小波变换系数模值图

图8-12　兰州站Morlet小波变换系数模平方图

图8-13　兰州站Morlet小波变换系数相位图

从图8-9中可分析出径流存在明显的年际变化和年代际变化，随着伸缩尺度a的增大（即分辨率的减小）不同尺度振荡的小波变换部分被分离开来。从上至下可分析得出径流存在30年以上尺度，10～30年尺度，7～17年尺度及10年以下尺度的周期变化，周期中心分别为38年、21年、15年，以下用丰 （枯）期中心分析周期变化，其结论更具体明确，并可与后面的相位分析结论一致。

从较大尺度38年分析，径流变化出现丰、枯交替的准2次振荡，对应于这种大尺度的丰枯交替，黄河上游径流变化表现出了明显的突变特征，具体表现为1929年以前偏枯，1930～1949年偏丰，1950～1969年偏枯，1970～1988年偏丰，1988～1997年偏枯，直到1997年等值线仍未闭合，1997年以后一段时间仍将处于偏枯期。

从21年尺度分析，径流出现准3次振荡，具体表现为1924年以前偏丰，1925～1935年偏枯，1936～1947年偏丰，1948～1958年偏枯，1959～1969年偏丰，1970～1980年偏枯，1981～1991年偏丰，1992年以后偏枯，而且这一偏枯曲线直到1997年仍未闭合，与30～40年尺度的变化一样，1997年以后一段时间仍将处于偏枯期。

30～40年和10～30年尺度的周期变化在整个分析时段表现得非常稳定，具有全域性。

15年尺度的周期变化具有局域性，主要在20世纪30～80年代表现活跃，存在负、正、负的周期振荡，具体为1932～1939年径流偏丰，1940～1946年径流偏枯，1947～1953年偏丰，1954～1961年偏枯，1962～1969年偏丰，1970～1977年径流偏枯，1978～1985年径流偏丰。大尺度下的一个丰期 （或枯期），包含小尺度下的若干个丰枯期。

对应于10年以下较小尺度的径流变化，较为明显的周期为1～5年尺度的年际变化，主要发生于20世纪40～70年代中期，70年代中期之后，周期中心上移，变为5～10年左右尺度的周期变化，到80年代中期，周期中心又下移到1～5年尺度，其他时间尺度的周期变化不明显。对于小尺度而言，径流突变点增多。不同时间尺度下，径流突变点个数、时间位置都有所不同，径流突变点应针对具体时间尺度来讨论。

从图的上部可看到存在30年以上的周期变化，随着径流资料序列的延长，可以分析出更大尺度的周期变化。

以21年尺度为例，各丰枯期的径流值与其小波系数的对照见表8-5，表中数据进一步表明小波系数的实部可以表征实际径流的丰枯相位变化，二者具有较好的对应关系。

表8-5　丰枯期径流与小波系数实部对应表　单位：亿m3

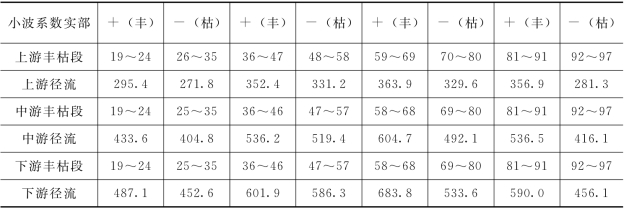
注 表中时段19～24代表1919～1924年，依此类推。

（2）小波系数虚部。

Morlet小波变换的实部和虚部可以作为两个小波函数对待，虚部是一个反对称小波函数，考虑小波变换的实部与虚部π/2的相位差，从图8-10分析所得结论与图8-9基本一致。

（3）小波系数模。

小波变换系数的模值表示能量密度，模值图把各种时间尺度的周期变化在时间域中的分布情况展示出来，小波变换系数的模值越大，表明其所对应的时段和尺度的周期性越明显。

从图8-11中可看出30～40年、10～30年尺度的小波变换模值较大，说明这两个周期变化最明显；其次是7～17年和10年以下尺度的周期变化。

（4）小波系数模平方。

小波系数模的大小不代表各种周期变化成分能量的大小，这与傅里叶分析是完全不同的，某一尺度的周期信号，其模值虽然很大，但实际上这些信号对整个原始信号的方差贡献是很小的，小波系数的模平方相当于小波能量谱，所以从小波系数模平方图可分析出不同周期的振荡能量，能量谱的分析比小波系数模的分析更全面客观，小波系数模不能直接用于能量的对比分析，而能量谱的结果则可以直接比较不同时间尺度振荡的强弱。

从图8-12中可看到，10～30年和30～40年尺度的周期非常显著，占据整个时段，能量最强，10年以下尺度的周期也比较显著，但10年尺度的周期变化具有局部化的特征。其他尺度的周期变化都较弱，能量较低。(www.xing528.com)

（5）小波系数相位。

小波变换系数的相位分布图显示信号的突变点或奇异点的存在及其出现的位置，图8-13表明，在大时间尺度范围内有几个较为明显的影响区域，等相位线从大时间尺度的较大的分布区域辐合到较小的时间尺度的很小的分布区域内，辐合点即突变点分别出现在1954年、1978年、1984年、1991年。

8.4.9.2　黄河中游小波变换结果及分析

图8-14～图8-18分别为三门峡站河川径流Morlet小波变换系数的实部、虚部、模、模平方、相位等值线图。

（1）小波系数实部。

图8-14从上至下，可分析得出代表黄河中游的三门峡站河川径流序列的变化具有30～40年、10～30年、7～17年及10年尺度以下的周期变化，周期从大到小呈现嵌套结构。

21年尺度的丰枯期的径流值与其小波系数的对照见表8-5。

（2）小波系数虚部。

考虑小波变换的实部与虚部π/2的相位差，可知图8-15与图8-14分析得出的径流变化周期一致。

图8-14　三门峡站Morlet小波变换系数实部

图8-15　三门峡站Morlet小波变换系数虚部

图8-16　三门峡站Morlet小波变换系数模值图

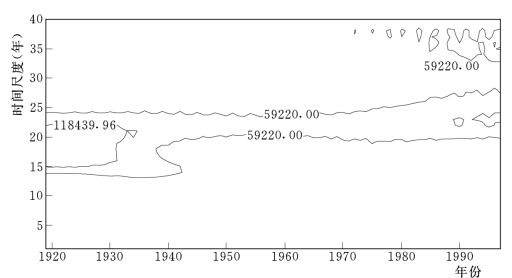
图8-17　三门峡站Morlet小波变换系数模平方图

图8-18　三门峡站Morlet小波变换系数相位图

（3）小波系数模。

从图8-16分析，模值最大的是10～30年尺度的周期，表明这一尺度的周期变化最明显，其次是30～40年和10年以下尺度的周期。

（4）小波系数模平方。

从图8-17可知，能量最强的是全域性的10～30年尺度的周期变化，呈条状分布在整个分析时段；30～40年尺度的周期变化，在20世纪80年代以后能量增强，与10～30年尺度的周期能量相当。

（5）小波系数相位。

图8-18显示，在21年时间尺度范围内有4个明显的影响区域，等相位线从大时间尺度的较大的分布区域辐合到较小的时间尺度的很小的分布区域内，突变点分别为1954年、1978年、1984年和1991年。

8.4.9.3　黄河下游小波变换结果及分析

图8-19～图8-23分别为花园口站径流Morlet小波变换系数的实部、虚部、模、模平方、相位等值线图。

图8-19　花园口站Morlet小波变换系数实部

图8-20　花园口站Morlet小波变换系数虚部

（1）小波系数实部。

图8-19从上至下，代表黄河下游的花园口站河川径流的变化具有30～40年、10～30年、7～17年及10年尺度以下的周期变化。

21年尺度的丰枯期的径流值与其小波系数的对照见表8-5。

（2）小波系数虚部。

小波变换的实部与虚部有π/2的相位差，从图8-20与图8-19分析得出的径流周期规律基本一致。

图8-21　花园口站Morlet小波变换系数模值图

图8-22　花园口站Morlet小波变换系数模平方图

图8-23　花园口站Morlet小波变换系数相位图

（3）小波系数模。

分析图8-21可知，10～30年尺度的模值最大，周期变化最明显；30～40年尺度的周期在20世纪80年代以前表现明显，10年以下尺度的模值与30～40年的相同。

（4）小波系数模平方。

从图8-22中看到，能量最强的是全域性的10～30年的周期，呈条状占据整个分析时段，它对原径流时间序列的方差贡献最大。

（5）小波系数相位。

分析图8-23可知，在21年时间尺度范围内有4个较为明显的影响区域，等相位线从大时间尺度的较大的分布区域辐合到较小的时间尺度的很小的分布区域内，辐合点分别出现在1954年、1978年、1984年、1991年。