随机序列功率谱分析成果

在实际工作中，我们研究的对象不仅仅局限于周期函数或非周期函数，更多的情况是时间序列的问题，时间序列是各种社会、经济、自然现象的数量指标按照时间次序排列起来的统计数据。因此，我们需要研究分析随机时间序列的功率谱，包括单个随机时间序列的谱分析和两个随机时间序列的谱分析。

随机序列的谱分析与函数的谱分析有很大的不同，首先，随机序列是一有限数列，函数的谱分析的频谱范围是无限的，而随机序列的频谱分析区间是有限的；其次，随机序列为离散数据，谱分析方法比解析函数复杂得多。

谱函数的类型较多，它们从不同角度和侧面反映波动时间序列的频域特征，主要有数据谱、功率谱和交叉谱。数据谱是数字时间序列自身相应的频域表示。功率谱是数字时间序列在不同频率上能量分布特征的表征。交叉谱是研究和表征两个时间序列在不同频率上相互关系的有效工具。由交叉谱派生出的各种谱函数能从不同角度来度量两个序列的频率关系。

目前，随机序列功率谱的计算方法主要有直接计算法、间接计算法和快速傅里叶变换计算法。这三种方法中，应用最广泛的是间接计算法。直接计算法与快速傅里叶变换法适用于编程计算。

8.3.5.1　功率谱的直接计算法

仿照傅里叶级数展开的计算，对于离散序列f（tj）（j=1，2，…，N），其傅里叶变换可写成

式中：ak和bk为傅里叶系数，k=1，2，…，M。因此

可见，直接计算法得到的是离散谱，所以又称为离散傅里叶变换，其计算步骤与谐波分析相同。

8.3.5.2　功率谱的间接计算法

间接计算法是以自相关函数的傅里叶变换为基础的，其计算方法比直接计算法简单，为一般谱分析普遍采用。

定义函数f（t）的自相关函数为

式中：τ为时间间隔，也称“时延”。(www.xing528.com)

如果以t=t1-τ代换式（8-21），则得

因此，R（τ）为偶函数。应用傅里叶变换定理，由式（8-21）可以推得

式中：E（ω）为函数f（t）的能量谱密度函数（简称能谱），它是自相关函数的傅里叶变换，而自相关函数则是能谱的逆变换。

因此

与函数的傅里叶变换相同，它们组成傅里叶变换对

由于R（τ）为实的偶函数，式 （8-23）进一步可改写为

式 （8-24）是能谱间接计算法的理论式，应用时还必须将其有限化和离散化

式中：k=0，1，2，…，m，m为最大时延，k为基本周期2m内的谐波波数。这时E（k）习惯上又称为功率谱，由式（8-25）可得到功率谱的估计值。

但是，应用式（8-25）得到的功率谱随着k值的变化一般起伏较大，故称为原始谱估计或粗估谱。因此，还要用所谓的“窗函数”或 “光滑系数”对其作平滑处理，才能求出 “精细”谱估计值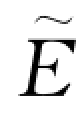（k）。常用的光滑系数有下面两种：

（1）哈明—图基（Hamming-Tukey）光滑系数