河流信息密码解读：上、下游径流协整系统的估计与检验

第一步：先用最小二乘法估计zt对xt的协整回归，包含常数项和趋势项，回归方程如下

式 （5-59）括号中的数据为对应系数的标准差，下同。

检验协整性其实就是检验协整回归，即式 （5-59）中的残差是否存在单位根。如果这两个序列不是协整的，那么这些残差中一定存在单位根，这就是非协整性零假设，如果这两个序列是协整的，那么残差将是平稳的。

应用Engle-Granger协整检验来检验上游径流序列xt与下游径流序列zt之间是否具有协整关系。

式 （5-59）的残差为

检验残差项εt的单位根，用Δεt对εt-1回归，仍然包含常数项和趋势项，回归方程如下

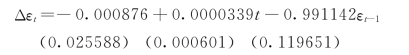
常数项和趋势项的系数很小，几乎为零，检验统计量值(www.xing528.com)

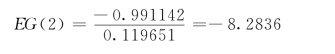
括号中2指协整回归中的变量数为2。

零假设为H0∶εt-1的系数为零，在1%的显著性水平下，两变量Engle-Granger分布的临界值为-4.3266 （见表5-19），而检验统计量的值为-8.2836，-8.2836＜-4.3266，因此拒绝非协整性零假设，认为zt与xt之间具有协整关系，协整向量为（1，0.972304）′。

表5-19　Engle-Granger协整检验临界值

注 表中数据摘自赵文奇.当代经济计量学中的协整理论.统计研究，1996 （6）：51-58。

第二步：用公式表述具有变量协整这一约束条件的动态过程，用误差修正表示法，对于两个变量xt，zt，误差修正方程为

式 （5-61）中ECt-1是式（5-60）产生的残差序列。