使用ADF单位根方法检验变量的平稳性，通过最小二乘法作自回归，自回归有三种模型，即模型（5-6-1）、模型（5-6-2）和模型（5-6-3）。
滞后变量的阶数p的确定采用SC法，计算p=1～5时的SIC检验值，见表5-2，经计算比较，p=3时，SIC（3）最小，所以上游径流序列的自回归阶数为3。
同理，由SIC法确定下游径流序列的自回归阶数，见表5-2，从表中数据可知，下游径流序列的自回归阶数也为3阶。
表5-2 滞后阶数与SIC检验值
零假设为H0∶ρ=1，对上游径流序列做回归，对应以上三种模型得到的估计分别见表5-3～表5-5，检验结果见表5-6。
表5-4 有截距无趋势模型参数估计（因变量：ΔXt）
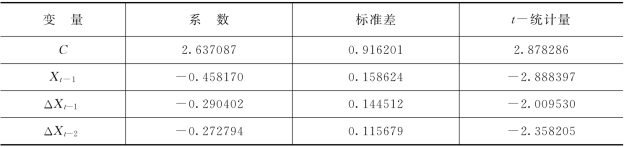
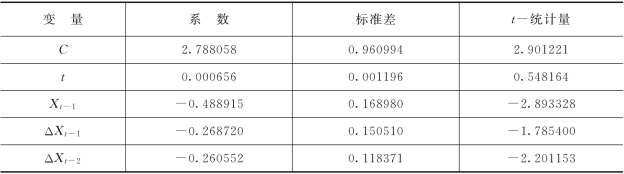
表5-5 有截距有趋势模型参数估计（因变量：ΔXt）
Dickey-Fuller检验的统计量ADF即是通常的t-统计量，用系数估计值除以对应的标准误差得到，即
当检验中包含常数项和趋势项时，1%显著性水平的ADF检验临界值为-4.04，5%检验临界值为-3.45，10%检验临界值为-3.15，而ADF统计量为-2.89，大于三个显著水平的临界值，可以显著地接受ρ=1的单位根零假设，即序列x存在单位根，是非平稳的，需要对x的一阶差分进一步做单位根检验（见表5-6，表中只给出了1%显著水平的临界值）。
表5-6 x序列单位根检验
一阶差分单位根检验的方法与上相同，计算结果见表5-7～表5-9，检验计算结果见表5-10。
表5-7 无截距无趋势模型参数估计（因变量：Δ2Xt）
表5-8 有截距无趋势模型参数估计（因变量：Δ2Xt）
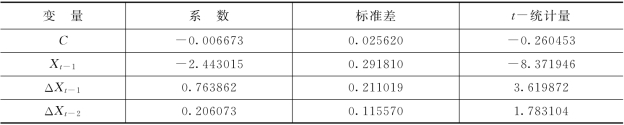
表5-9 有截距有趋势模型参数估计（因变量：Δ2Xt）
(www.xing528.com)
表5-10 x一阶差分序列单位根检验
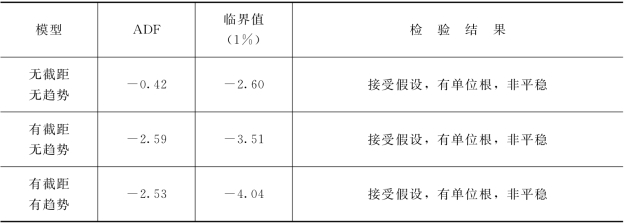
表中数据表明，三种模型的ADF值均小于其临界值，x一阶差分是平稳序列，即x是一阶平稳的，x ～I（1），Δ（x）～I（0）。
下游花园口径流序列z的单位根计算结果见表5-11～表5-13，检验结果见表5-14，三种模型的ADF统计量均大于1%显著水平的临界值，因此序列z是非平稳的。
表5-11 无截距无趋势模型参数估计（因变量：ΔXt）
表5-12 有截距无趋势模型参数估计（因变量：ΔXt）
表5-13 有截距有趋势模型参数估计（因变量：ΔXt）
表5-14 z序列单位根检验
z一阶差分序列单位根计算结果见表5-15～表5-17，检验结果见表5-18。
表5-15 无截距无趋势模型参数估计（因变量：Δ2Xt）
表5-16 有截距无趋势模型参数估计（因变量：Δ2Xt）
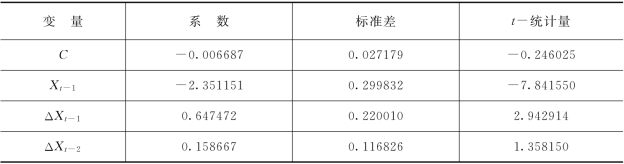
表5-17 有截距有趋势模型参数估计（因变量：Δ2Xt）
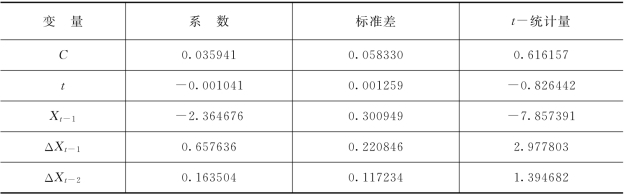
表5-18 z一阶差分序列单位根检验
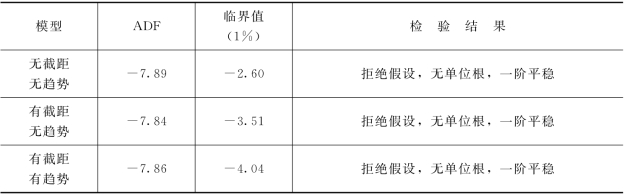
同样，三种模型的ADF值均小于其临界值，z一阶差分是平稳序列，即z是一阶平稳的，z～I（1），Δz～I（0）。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
