河川径流信息密码解读理论与实践：F检验法的应用

在统计学的回归分析中，通常用F检验来考察两个回归模型是否有显著差异，以确定某些自变量是否有留在模型中的必要。实际中F检验也常被用来考察两个ARMA模型之间是否有显著差异，进一步判定ARMA模型的阶数。具体的做法是：先给模型定一个较高的阶数，假定模型中的某些高阶参数为零，再用较低阶的模型重新拟合，然后通过F检验考察降低阶数之后的模型与原来的高阶模型之间是否有显著差异。如果差异显著，则那些假设为零的高阶参数有保留的必要，即原假设不成立，模型阶数还有升高的可能。如果差异不显著，则说明原假设成立，高阶参数为零，用低阶模型拟合就可以了。再重复以上方法继续判断模型的阶数是否还有再降低的可能，直至模型阶数再也不能降低为止，此时的阶数就是模型的适合阶数。

考虑如下线性回归模型

可以证明，统计量F服从自由度为s和N-n的F 分布，即

式中：n为模型阶数总数；s为被检验的阶数差数；N 为观测数据总数。对于预先给定的显著性水平α，查F分布表（见附表3），满足

5.4.3.1　AR（p）模型定阶的F准则

1967年，瑞典控制论专家K.J.Astrom教授将F检验准则用于对时间序列模型的定阶。设Xt（1≤t≤N）是零均值平稳序列{Xt，t=0，±1，…}的一段样本，并用模型AR（p）

而模型AR（p-1）的残差平方和为

(www.xing528.com)

可以证明，统计量F服从自由度为1和N-p的F 分布

5.4.3.2　ARMA（p，q）模型定阶的F准则

仿照AR（p）模型定阶F检验准则，可以将F检验应用于ARMA（p，q）模型的定阶。采用过拟合方法，首先对观测数据用ARMA（p，q）模型进行拟合，再假定φp，θq高阶系数中某些取值为零，用F检验准则来判定阶数降低之后的模型与ARMA（p，q）模型之间是否存在显著性差异。如果差异显著，则说明模型阶数仍存在着升高的可能性；若差异不显著，则说明模型阶数可以降低。低阶模型与高阶模型之间的差异用残差平方和来衡量。

设有零均值随机序列{Xt，t=0，±1，…}，用自回归滑动平均混合模型ARMA（p，q）来拟合，模型AR部分的参数满足平稳性条件，模型MA部分的参数满足可逆性条件

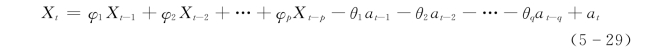
ARMA（p，q）模型的残差平方和为

统计量F服从自由度为2和N-p-q的F 分布

n=p+q表示模型阶数的总数；s=2表示被检验的参数总个数。如果F＞Fα，则H0不成立，模型阶数仍有上升的可能；否则H0成立，即ARMA（p-1，q-1）是合适的模型。