奇妙数学世界：勾股数的求法

在不定方程xn+yn=zn(n∈N+)中,当n=2时,x2+y2=z2 是在初二时就学过的勾股定理.即勾(较短直角边)方加股(较长直角边)方,等于弦(斜边)方.“勾3股4弦5”是最简单的一组勾股数.对勾股数组的研究,在数量方面是研究不定方程x2+y2=z2 的整数解的问题,在图形方面是研究构成直角三角形的条件.我们采用由个别到一般的方法,研究勾股数组.

下面给出勾股数组的几种求法:

从最简单的一组勾股数组3,4,5说起:

(1)最简单的勾股数组3,4,5的任何正整数倍,仍是勾股数组.

例如:6,8,10是3,4,5的2倍,它们仍是一组勾股数,9,12,15;12,16,20等也都是勾股数组.我们把类似于3,4,5的情况,即三个数之间无公约数的数组,叫作不定方程x2+y2=z2 的基本解,而把6,8,10;9,12,15,即3,4,5的倍数(m∈N+)叫作不定方程x2+y2=z2 的非基本解.

(2)当勾是奇数时,勾的平方拆成相邻两个数的和,勾与勾的平方拆成相邻的两个数构成一组勾股数.

例如:∵32=9,9=4+5 ∴3,4,5是一组勾股数.

∵52=25 25=12+13 ∴5,12,13是一组勾股数.

∵112=121, 121=60+61, ∴11,60,61是一组勾股数.

如果勾是n(n 是奇数),则股是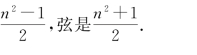

例1 在直角三角形中,最小的直角边(勾)是13,求:股和弦

∴股是84,弦是85

(3)当勾为偶数时,设n 为奇数,则2n 为偶数,把n 为奇数时的勾股数组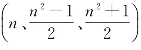乘以2.就是勾是偶数时的勾股数组(2n、n2-1、n2+1).

例2 在直角三角形中,勾是12,求:股和弦(www.xing528.com)

解:∵2n=12 ∴n=6.

则股=n2-1=62-1=35,弦=n2+1=62+1=37,

∴这组勾股数为12,35,37.

(4)当n、m∈N+,则n2-m2,2mn,n2+m2(n＞m)组成勾股数组.

即 (n2-m2)2+(2nm)2=(n2+m2)2.

(5)设x,y,且m=x,n=2y+x-1,代入(4)得:

勾:(2y+x-1)2-x2;

股:2(2y+x-1)x;

弦:(2y+x-1)2+x2.

练习

1.在直角三角形中,求:勾分别为15,17,19,21的股和弦;

2.在直角三角形中,求:勾分别为16,18,20,22的股和弦.