数学世界之奇妙0的到来

我们经常采用一些假定的符号和词语,可你要知道数学中的大量符号都是经过千百年的演化而形成的,并为人们逐渐习惯了的.词语“零”和数字“0”提供了这类演化最好的例子.现在通用的1～9这几个数字叫作阿拉伯数字,从印度传入阿拉伯然后传入中国的.我国古代并不用这些数字,就是外国也不是一开始就用阿拉伯数字的.如古罗马用的数字就是:Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ,Ⅵ,Ⅶ,Ⅷ,Ⅸ,分别代表1,2,3,4,5,6,7,8,9.

这在现代一些钟表的面儿上也有出现.

“0”是数学史上的一大发明,其意义非同小可.“0”代表“无”,没有“无”,何来“有”.因此“0”是一切数的基础.其次,没有“0”就没有进位制,没有进位制就难以表示大数,数学就没有发展.“0”的特点还表现在其运算功能上:任何数加减“0”,其值不变;任何数乘以“0”都得“0”.“0”的原型是什么? 是一无所有吗?

随着十进位制记数法的产生和发展,零的符号就不再是可有可无了.我国古代用算筹计算时,人们采用不放筹的办法来表示缺位.随着数学的发展,演算过程越来越复杂,只靠空位或空一段距离的办法已不能明确表示数了.

在历史上,“0”这个符号的创造还兜了个有趣的圈子.中国数学家用表示该写“0”的空位,这方法传到了印度,印度演变成“0”的形状,又传到阿拉伯,再从阿拉伯传入中国.我们现在所讲的十个阿拉伯数字,其实都是印度传过去的,而“0”的老祖宗,还要算我们中国的呢!

“0”的创造,在数学史上确是一个重大发展.在许许多多的科学发明当中,“0”的发明简直和印刷术、电话、汽车、火车等发明一样重要.数码添加了“0”,记载各种各样的数就方便多了.有个顺口溜说得好:“十个数字十兄弟,千变万化真有用.组成数目无限量,缺少一个不成功”.这样,数码也就由原来的九个增加到十个.

还有个要明确的问题:“0”是自然数吗?

对于0是不是自然数历来存在两种规定,我国过去的大、中、小学教科书中,都规定“0”不是自然数.为什么现在的小学教材中规定“0”也是自然数了呢? 这是因为大多数国家的教科书中,都规定了“0”是自然数,为了方便与国际上的交流,我国曾在1993年12月发布,从1994年7月1日起实施的《中华人民共和国国家标准——量和单位》中规定:“0”是自然数.2000年后出版的教科书中,都规定“0”是自然数.对我们来说,应该遵照这个规定.

【阅读与欣赏】

数学回文

一提到李白,人们都知道这是我国唐代大诗人.如果把“李白“两个字颠倒一下,变成“白李”,这也可以是一个人的名字,此人姓白名李.像这样,正着念、反着念都有意义的词语叫作回文.

文学史上有很多与回文有关的故事.在清代,北京有个酒楼叫“天然居”.一次乾隆皇帝触景生情.以酒楼为题写对联,上联是:

客上天然居,居然天上客.

但是,这位博学多才的皇帝苦苦思索,却写不出下联.因为下联的后五个字,必须是上联的前五个字的颠倒.又要语意通顺,还要平仄协调,的的确确是很难的事.直到很久以后,才有位和尚给出了下联:

僧游云隐寺,寺隐云游僧.

与此类似,数学里也有“回文式”.

我们借用上面的对联组成这样一个式子:

僧游×云隐寺=寺隐云×游僧

现在要问:不同的汉字用不同的数字(0～9)代替,这个算式能成立吗? 能,而且不止一个:

我们看到,这类等式不但外形整齐、对称,内部构造也很巧妙:每个等式中的两位数的十位数字和三位数的百位数字的乘积正好等于两位数的个位数字和三位数的个位数字的乘积;等式中三位数的十位数字恰好等于百位数字与个位数字的和.例如:12×231=132×21中,1×2=2×1,3=2+1;在12×693=396×21中,1×6=2×3,且9=6+3.

掌握了这两个特点,就容易写出这类等式了.并容易看出,关键是找出满足第一个条件的四个数字,从而三位数的十位数字也就确定了.例如,3×6=9×2,这时三位数的十位数字是6+2=8,可得等式:(www.xing528.com)

当然,也可以由9×2=3×6,且2+6=8,得到:93×286=682×39.

这两种形式反映了同样的四个数之间的关系,可以看作是一个等式的两种形式.那么这类等式共有多少个呢?

我们可以从1开始,依次取2,3…,9进行组合,然后再从2开始,依次取3,4…,9,进行组合.看能组成多少不完全相同的4个数字的乘积,并且第2、第4个数字的和不大于9.

以此类推,共可得到33个不同的等式.

数学里还有“回文数”,其特征是:从左到右读与从右往左读完全一样,例如,101,32123,9999等.

两个相同位数的回文数,如果各位相加时能够“就地消化”,不发生进位情况,那么其和仍是一个回文数.同样在两个回文数相减时(规定要用大数减小数),如果不需要从上一位“借”,则差也是回文数.例如:

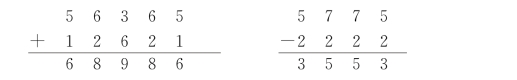
有趣的是,某些回文数在相加时即使要发生“进位”,但其和数却依然是个回文数.例如:

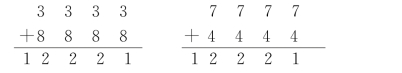
这样的回文数的模式是(共有n 个a)与bbb……b(共有n个b),而且a 与b 应满足关系a+b=11,以及1＜a＜10,1＜b＜10.

假如你遇到一个不是回文数的普通数,怎样才能使它“变”成回文数呢? 办法很简单,只要把这个数加上它的逆序数就行了,这称为一次“操作”(或“变换”).把这种“操作”反复进行下去,到头来就可以得到一个回文数.

这就是有名的“回文数猜想”.它至今仍是个谜,因为如果说它正确,却至今无法证明;如果说它不正确,又找不出一个反例.

可能成为说明“回文数猜想”不成立的反例是196,因为有人用电子计算机进行了几十万步的计算,仍然没有出现回文数,但是却没有人能证明这个数永远产生不了回文数.

数学家还对“回文质数”进行了大量的研究,发现了另外一些“谜”:101,131,353,919,这些自然数既是回文数,又是质数,叫作“回文质数”.

第一个谜是:“回文质数”有无穷多个吗? 数学家猜想它有无穷多个,但也仅仅是猜想.

像181和191,373和383,30103和30203等,他们都是“回文质数”,并且每一对中间的数字是连续的,而其他数字都是相同的,这样的两个数叫“回文质数对”.

第二个谜是:回文质数对有无穷多个吗? 至今也没有解决.

数学家还发现,在回文数中,平方数是非常多的,例如:112=121,1112=12321,11112=1234321,…,1111111112=12345678987654321.

立方也有类似情况,例如:113=1331,1113=1367631.