超炫漫话-定积分、费曼积分和留数的鲜为人知之处

首先从恒力做功说起。一位农民赶着马车去京城卖菜，路途10 千米，车上装着800 棵白菜，每棵4 千克，马车自重150 千克。设路面与车轮间的摩擦系数为0.3。农民徒步前进，马儿往返应做多少功？

恒力作工，去程：

返程：

总功：

从菜园到京城，道路崎岖，需要爬坡。农民坐在车上，设车前进的阻力f 与路面x的关系为f=0.1x2-0.3x+50，其他情况与上面相同。仅去程马儿应做多少功？

这是变力做功，需要积分，计算过程如下：

积分分为三大类：普通积分、费曼积分、复变函数积分。普通积分又分不定积分和定积分（积分、二重积分、三重积分），线积分、面积分、体积分。例如，不定积分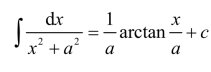表示已知原函数的导数求原函数的运算，这种原函数有无数个，它们仅仅相差一个常数。而二重积分表示以区域D 为底的曲顶柱体的体积，可以将这类积分化为二次积分：

三重积分是在闭长方体上对某三元函数f（x，y，z）的积分，可以转化为三次积分，

定积分与不定积分之间的联系是牛顿-莱布尼兹公式：

例如，求曲线　xy sin=在[0，π]上与x 轴所围成的面积

还有曲线积分、曲面积分等，这里不再赘述。

费曼首次在量子理论中引入了路径积分，所以量子理论以及超弦理论中的路径积分又称费曼积分。量子理论刚建立时，遇到了如何将约束系统量子化的问题。欲建立电磁场以及电磁相互作用的微观理论，需要将其量子化。约束系统量子化的方法有两种：狄拉克正则量子化方法和法捷耶夫——波波夫提出的、费曼发展起来的路径积分量子化方法。前者是从经典分析力学出发，考虑量子条件，根据正则坐标qi、在正则动量Pi、、哈米顿H（qi，Pi，t），中利用泊松括号导出正则动量的泊松括号，从而导出正则运动方程，使经典系统过渡到量子系统。后者是用量子态代替运动路径。从X 到Y 传播的粒子，传播路径很多，可以认为无限多，到底经历了哪条路径？都有可能。费曼假定，各种不同的可能路径具有相等的概率，只是相位不同。表达出与路径X（t）相应的作用量，则可以写出概率振幅。然后由叠加原理对所有路径上的振幅求和，和的模平方就是粒子从0q 到q的概率：(www.xing528.com)

而粒子波从0q到q的概率振幅就由下面的表达式来表示：

当t→0，n→∞时，上述n重积分变成了无穷的重积分，即路径积分。两种方法各有千秋，但是一般多用费曼积分法。

复变函数可分为解析函数和非解析函数两大类，而积分路径可分为非闭合和闭合两大类。所以，复变函数的积分可以分为四种情况：①解析函数沿着非闭合路径的积分；②非解析函数沿着非闭合路径的积分；③解析函数沿着闭合路径的积分；④非解析函数沿着闭合路径的积分。

首先谈谈复变函数的积分定义。复平面上有一条曲线C，A、B 分别为始点和终点，取n-1 个分点将曲线任意分成n 段，每一段的长度为Δzn，该小段承载的函数（密度、截面积、电阻率等）f（ξn）看作常数，则所有各段长度与承载函数的乘积之和，在n→∞ 时的极限叫作复变函数的积分，记作

如果C 是闭合曲线，则记作；如果f（z）是连续的而C光滑或分段光滑，则积分一定存在。设

则有复变函数在一般情况下的普遍积分公式 ：

或者将被积表达式参数化：

例1 计算复变函数的积分∫CRe Z dZ，这里C 是抛物线y=2x2上从坐标原点到点（2，8i）的一段曲线弧。本题首先将被积表达式参数化：令x=t，y=2t2，于是有

解析函数沿着闭合路径的积分，这是上面谈到的第三种情况。柯西定理告诉我们，区域B 是单连通域，复变函数在B 内处处解析；C是B 内的任意闭合曲线，则复变函数沿曲线C的积分总是零，即

第四种情况，非解析函数沿着闭合路径的积分。非解析函数在闭合路径C 内一定存在奇点，一个、两个……我们把这些奇点围起来或者盖上帆布，并在旁边树立木牌，上写“此处凶险，切莫靠近”，行人就可以安然无恙了！在屏蔽了奇点的闭合路径内，原来的非解析函数就变成了解析函数。根据第三种情况的结论，积分结果应该为零。问题是，如何将闭合路径内的奇点屏蔽起来？屏蔽之后，如何处理？前一个问题，将闭合路径内的各个奇点用顺时针方向的小圆周包围起来；后一个问题，沿着每一个顺时针方向的小圆周C1，C2，…Cn进行积分，然后累加，相加的结果正是非解析函数沿着闭合路径C的积分。即非解析函数沿着闭合路径的积分等于沿着闭合路径内包围奇点的围道（顺时针）积分之和。

解析函数沿着非闭合路径的积分，属于第一种情况。该情况下，积分与路径无关，仅仅与始点和终点的位置有关。这与普通积分一样，可以用牛顿-莱布尼兹公式计算。第二种情况不再赘述。