超炫漫话：泊松与泊松括号精要

泊松，法国人（1781—1840），著名数学家和物理学家。1798年在巴黎综合工科学校学习，因为头脑聪明、成绩优秀而深得拉普拉斯和拉格朗日的喜爱。1800年他被留校任教，后来升任副教授、教授。1821年，他当选为法国科学院院士。泊松先生擅长用数学手段研究物理问题，对电磁理论、理论力学、概率论、热学、弹性理论、行星运动、数学积分都有重要贡献。以他的名字命名的数学、物理概念有泊松定理、泊松方程、泊松分布、泊松积分、泊松括号等。泊松括号在超弦理论中应用广泛，现在就泊松括号向读者做一简要介绍。

如果A 和B 都是正则变量和时间的函数，A=A（qα，pα，t），B=B（qα，pα，t），t 为时间，qα，pα都是正则变量，则A、B 构成泊松括号

所谓正则变量是满足正则方程组的两组变量相互正则共轭，组成正则共轭变量，简称正则变量。三个基本泊松括号皆为零：

类似的，

泊松括号有以下性质：

（1）[A，C]=0　C 为常数。

（2）C[A，B]=[CA，B]=[A，CB]。

（3）[A，B]=-[B，A]。

（4）[-A，B]=-[A，B]。

（5）

（6）满足加法、乘法结合率。

设W 是某力学量，将该式对时间求导，得(www.xing528.com)

将哈密顿正则方程代入上式，可得

将W 换做qα，pα，分别得到

式中H 是哈密顿，qα、pα分别是广义坐标和广义动量。雅可比恒等式为

超弦理论中，定义能量-动量张量为 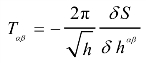，由于δ s /δhαβ=0，故Tαβ=0。这意味着能量守恒。如果用泊松括号，则有

物态≥0，所以上式左边为0，而右边第一项为0，第二项必须D=26 才为零。由此导出开弦的维尼齐亚诺模型，以及闭弦的维拉宿模型只有在26维空间才具有物理意义。

不仅如此，弦坐标的泊松括号以及弦坐标对于变量τ的泊松括号皆为零：

将超弦看作谐振子，其坐标的泊松括号是

弦的能量-动量张量的傅立叶模Lm 计算十分重要。Lm 又称为维拉宿算子，它的泊松括号为

该式最终可化为下面的形式

可见，超弦理论之所以令人信服，在于严谨的逻辑论证。而泊松括号的重要作用由此可见其普遍性。