人们常说，“物以类聚，人以群分”，“秋天到了，天气凉了，一群大雁往南飞”。什么是“群”呢？群，就是具有某种共同性质的事物的全体。黑猪，白猪，花猪，张家的猪，王家的猪，构成一个“猪群”。正整数、负整数，以及零，构成一个“整数群”。
确切地说，群的定义如下。
设有集合G=｛a，b，c，…｝和G 上的二元运算，如果满足下列条件。
（1）封闭性。若 a，b∈ G，则c=a·b∈G，即两个任意元素的乘积仍在群之内。
（2）结合律。（a ·b）· c=a ·（b ·c），即三个群元素相乘，可先乘其中的两个。
（3）存在单位元。对G的任何元素a，有a·e=e·a，e叫作单位元。
（4）存在逆元。对G的任何元素a，总有b∈G，使得a·b=b·a=e，则称b 是a的逆元，记作 a-1。(www.xing528.com)
则称集合G 是一个群。例如，+1 和-1两个数字构成一个群。有理数群=｛正整数、正分数、负整数、负分数、零｝，因为这个群的元素满足封闭性和结合律，并且具有单位元1，不论正整数、正分数、负整数、负分数，还是零，都存在逆元，满足群的定义。
SU （2）群是行列式为1的2×2 复幺正矩阵构成的群。设2 行2 列矩阵为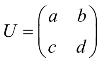
，a，b，c，d皆为x+iy形式的复数，所以2×2复矩阵共有8个参数。（2）US群的群元素有以下约束条件：第一，detU=1；第二，1U+U=。根据第一个约束条件，
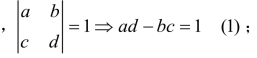根据第二个约束条件，
，可导出下述四个方程：
（5）四式构成约束条件。由于（1）和（4）为复数方程，（2）和（5）是实数方程，所以共有六个实数方程。由（4）（5）两式分别得出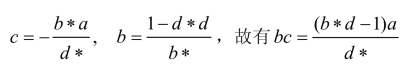 
。代入（1），可得*=da；同理可得*-=bc。由这两个等式以及（4）式，可得（1）式。所以6个实数约束方程实乃5个。8-5=3，因此SU（2）矩阵由3个独立参数确定，一般形式可以设为
而SU（2）群的一般定义
SU（3）群是行列式的值为1的3×3 复幺正矩阵构成的群。设3 行3列矩阵为
，a，b，c，d皆为x+iy 形式的复数，所以3×3复矩阵共有18 个参数。SU（3）群的一般定义为
1859年清代数学家李善兰与英国数学家合译了一本书，书名叫作《代数学》。大家学习过中学代数吧，方程和代数式，有理数、无理数、实数、复数的六则运算统统是代数，是初等代数。代数是研究数字和文字的代数运算的理论和方法，或者说，是研究实数、复数以及以它们为系数的多项式代数运算的理论和方法。
什么是超代数呢？我的理解是，超代数就是超空间中的近世代数。超空间，是坐标能够以普通数字和格拉斯曼数字描述的空间。近世代数，是近现代发展起来的，研究包括向量、矩阵、张量、旋量、群、环、域、顶点算子、泊松括号等性质及其计算法则的理论和方法。将近世代数推广到维拉宿代数、洛伦兹代数、超庞加莱代数、克利福德代数、流代数等，以研究超杨-米尔斯场和超空间、超对称、超弦。超代数是一把数学利器，是当代科学技术发展的需要。正如封建时代的小农经济使用锄头、镰刀，到了现代社会，使用播种机、联合收割机一样，研究超弦理论，数学先行，就非用超代数不可！其中，群的使用率最高，所以我们对于“群”应该略知一二。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
