各向异性随机场的样本轨道连续性

设是一定义在概率空上的值可调和算子尺度stable随机场，其定义如下：

其中Z1（t），…，Zd（t）是独立同分布于X（这里X由（7.1.1）式所定义）。在本节中，将研究值可调和算子尺度stable随机场Y局部时存在和联合连续的充分条件。

先回顾下随机场的局部时定义。随机场Z在I上的逗留时定义为：

如果μ关于上Lebesgue测度λd绝对连续，则称X的局部时（记为存在且满足：

因此是逗留时μ的密度，并称这里的x为空间变量，而称I为时间变量。注意，如果X在I上的局部时存在，则对I的任意Borel子集T，L（x，T）也是存在的。关于随机和确定向量场局部时的很好综述可参见Geman和Horowitz（1980）。也有许多学者研究自相交的局部时及其性质（见Geman等人（1984），Hu和Nualart（2005），Rosen（1987），Wu和Xiao（2010））。

设是一个固定矩形，如果局部时存在一个版本，仍记为使得它是关于变量是连续的，则称X在T上具有联合连续的局部时。当局部时是联合连续时，它将是随机场Z的水平集上的一个自然测度。这使得局部时成为一个有用的研究工具，可以用来研究与随机场Z的水平集和逆向集相关的各类分形性质。因此，关于局部时存在性和联合连续性的研究，以及用它们来研究随机场的分形性质，已经取得大量的结果。关于这方面的成果，可参见Ehm（1981），Xiao（1997），Xiao和Zhang（2002），Ayache等人（2008），以及Wu和Xiao（2011）。最近，陈振龙和肖益民（2019）研究了一类分量近似独立且满足某种强局部不确定性Gauss场局部时的联合连续性。

下面给出后文要用到的局部时的几个性质。

（i）局部时存在一个可测的修正，且满足下面的逗留时密度公式：对每个Borel集以及每个可测函数都有

（ii）局部时有下面的n阶矩公式（见Geman和Horowitz（1980）文中的（25.5）和（25.7）式）：对任意的和任意的整数n≥1，有

以及对任意的偶数n≥2有

其并且每个关于坐标分量将记为

下面的定理给出了随机场Z局部时存在的充分条件。

定理7.4.1　设是如（7.4.1）式所定义的可调和算子尺度stable随机场，当q＞dH时，则对任意的闭矩形随机场Z在T上存在局部时有如下的L2表示：

其中

证明　由Geman和Horowitz[40]的（21.9）式（也可见Adler[1]定理8.6.2）可得，对任意的闭矩形随机场Z在T上存在满足（7.4.5）式的局部时的充分必要条件是

从而只需要证明

事实上，利用Z1，…，Zd的独立性和（1.2.5）、（1.2.6）和（7.2.1）式有，

由所以

由引理7.3.2可推得（7.4.6）式的左边（LHS）小于

其中r0=sup{τE（s-t）：s，t∈T}，而最后一个不等式由引理1.2.9和r0的定义可得。显然当q＞dH时，有由此和（7.4.9），（7.4.10）式，可得（7.4.7）式成立。故定理7.4.1得证。

注7.4.2　本文仅给出局部时存在的充分条件，其实也可得到局部时存在的必要条件。即，如果随机场Z的局部时时存在，则dH＜N（ap+δ），这里δ由引理1.2.8所定义。但是这个必要条件并不是最优的，我们猜测局部时存在的必要条件是dH＜q，然而目前我们还无法证明。

下面的定理是本章的第二个主要结论，其给出了局部时具有联合连续性的充分条件。证明方法是基于Nolan（1989）对stable随机场局部时联合连续性的证明思想。

定理7.4.3　设是由（7.4.1）式定义的可调和算子尺度stable随机场，如果q＞dH，则对任意的闭矩形随机场Z在T上具有几乎处处联合连续的局部时。

为了证明定理7.4.3，需要下面的两个引理，这两个引理给出了局部时n阶矩的上界。为了符号上的简洁，令表示在度量τ下，中心在a，半径为r的闭球。

引理7.4.4　设是由（7.4.1）式定义的可调和算子尺度stable随机场，如果q＞dH，则对任意的闭矩形存在一个仅依赖于N，d，H和T的常数c7，4，1，使得对任意半径小于1的闭球以及任意的整数n＞1有

证明　由于是正的且满足（7.4.3）式，所以

利用变量替换un=vn，uj=vj-vj+1，j=1，…，n-1，可得

其中倒数第二个等式由Z1，…，Zd的独立性可得，最后一个等式由（1.2.4）—（1.2.6）式可得。

下面将利用随机场X的局部不确定性来证明（7.4.13）式中的积分是有限的。然而，局部不确定性仅在（7.2.5）式且该式中的点要充分靠近的条件下才成立。因此，先做一简化：固定一个n＞1，Dn能够用更小的集合来替代，这里δ是一充分小的正常数（见定理7.3.1）。这一简化是充分的，因为Dn可由有限个诸如S的集合构成（仅仅t1，…，tn的排列顺序不同）。只要能够证明（7.4.13）式中的积分在这些小区域上的积分是有限的，则其在Dn上也是有限的。因此从现在起，不妨假设X在Dn上是具有局部不确定性的，这是因为Dn总是可以划分为更小的区域，而在这更小的区域上局部不确定性是成立的。由上述讨论和（7.3.1）式，（7.4.13）式中的最后一个积分小于(www.xing528.com)

由引理7.3.2可推得（7.4.14）式中的最后一个积分小于

再做一次变量替换式等于

因为对所有的所以联合（7.4.13）—（7.4.16）式，推得

由于D是凸集，τE（t）是对称（即τE（-t）=τE（t））和连续的，且当

时，当时，所以

由引理1.2.9可得

利用（7.4.19）式，并按dtn，…，dt1顺序进行积分可得

这就证明了引理7.4.4。

引理7.4.5　设是由（7.4.1）式定义的可调和算子尺度stable随机场，如果q＞dH，则对每个闭矩形存在一个仅依赖于N，d，H和T的常数c7，4，1，使得对任意半径充分小的闭球所有满足所有偶数n＞1，以及所有充分小的γ∈（0，min{1，（q-Hd）/2H}），有

证明　由（7.4.4）式知

利用基本不等式可得

联合（7.4.22）和（7.4.23）式有

将（7.4.24）式中的内积分记为J，并通过变量替换un=vn，uj=vj-vj+1，j=1，…，n-1可得

由于对任意的j和γ∈（0，1），恒成立所以

其中φn∈{0，1，2}，求和符号是对所有序列（k1，…，kn）∈{1，…，d}进行的。由此及（7.4.26）式有

为方便起见，将（7.4.27）式中的积分记为J1。由Z1，…，Zd的独立性可推得

其中最后一个等式由（1.2.4）—（1.2.6）式可得。

正如在证明引理7.4.4时可假设随机场具有局部不确定性那样，这里也将假设Zj在Dn上也具有局部不确定性。从而由Zj的局部不确定性（见定理7.3.1）可得

其中第二个不等式由引理7.3.2可得。

现在通过另一个变量替换…，n有

因为对任意的j=1，…，d有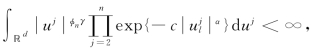所以联合（7.4.24）—（7.4.30）式可得

其中最后一个不等式通过类似于计算（7.4.18）—（7.4.20）式的方法可得。由于r＜1，φn≤2，所以

因此引理7.4.5的证明完成。

下面可以给出定理7.4.3的证明。

证明　虽然引理7.4.4和引理7.4.5中关于局部时高阶矩的估计是针对时间变量落入开球Bτ（a，r）内进行的，但是由这两个引理可得当时间变量落入矩形区域内的局部时高阶矩的估计。事实上，由引理1.2.8可推得，如果从而

因此利用引理7.4.4和引理7.4.5可得当时间变量落入矩形区域内时，局部时高阶矩的估计如下：

故定理7.4.3的证明由（7.4.33）式和（7.4.34）式，以及Kolmogorov连续性定理的多参数版本（见Khoshnevisan（2002））可得。由于剩下的证明部分与Xiao（2009）（也可见Xiao和Zhang（2002），或Wu和Xiao（2011））的定理8.2类似，所以这里略去具体的证明，从而定理证毕。