各向异性随机场X的Hausdorff测度确定

本小节主要确定随机场X像集的Hausdorff测度。下面的定理是本节的主要结论，其证明方法是基于Talagrand（1995）对类似问题的处理思想，也可参见Xiao（1997）和Luan和Xiao（2012）。

定理6.3.6　设是一（N，d）-高斯随机场，且满足条件（C1）—（C3）。如果对某个1≤k≤d，

则其中α0=0，则存在常数c6，3，10＞0，c6，3，11＞0使得

其中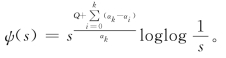

为了不使定理的证明过于冗长，先给出几个引理和命题。对任意的r＞定义X（t）在球B（y，r）内的逗留时如下：

如果y=0，则把T0（r）简写为T（r）。

引理6.3.7　如果（6.3.19）式成立，则存在一个正常数c6，3，12使得

其中

证明　当n=1时，由Fubini定理，极坐标变换和条件（C1）—（C3）可得

将（6.3.20）式中最后一个积分记并将其积分区间（0，∞）划分为则

当时，可得

当Q=且αk-1=αk时，可得

因为r充分小，所以

由此及（6.3.20）—（6.3.22）式，有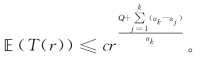

当n≥2时，利用全期望公式计算

由于当j=1，…，n时，t1，…，tn∈I，而当j≠k时，tj≠tk，所以

其中t0=0。因此

从而

故可得

这就证明了引理6.3.7。

注6.3.8　在证明引理6.3.7时，利用了条件（6.3.19）。现在考察另一种情况，即在这种情形下，上述方法可得到E

从而可证

其中但是由此还无法确定函是否是X像集的确切Hausdorff测定函数（见Pruitt和Taylor（1969）或Xiao（1997）的论述）。

命题6.3.9　如果（6.3.19）式成立，则存在常数b∈（0，1/c6，3，12）（常数c6，3，12如引理6.3.7中所定义）使得

其中

证明　由Fubini定理、泰勒展开式和引理6.3.7可得，存在正常数c6，3，12，使得对任意的0＜b＜1/c6，3，12有

利用Chybeshev不等式和（6.3.30）式有，对任意的∈＞0，(www.xing528.com)

现在令rn=e-n/logn，则对每个0＜δ＜1，以及n充分大有，

由Borel-Cantelli引理和事实知

由于r充分小时，ψ（r）是单调非降的，以及当n→∞时，ψ（rn）/ψ（rn-1）→1，所以

这就证明的命题6.3.9。

下面将证明本节的主要定理（定理6.3.6）。证明分为两部分，一部分证明下界，另一部分证明上界。

下界的证明

由于具有平稳增量，所以由命题6.3.9可得，对固定的t0∈I有

下面定义像集X（I）上的一个测度μ。对任意的Borel集令则且

设且（6.3.37）式成立}，则由Fubini定理知E⊆X（I）且μ（E）=1 a.s.。

由此及引理6.3.2，可得ψ-m（E）≥cb＞0 a.s.。

上界的证明　当l≥1时，令

则由引理6.3.5得

令其中

是上的Lebesgue测度。下面证明因为所以由Chebyshev不等式和Fubini定理有

显然因此由Borel-Cantelli引理可得即，

另一方面，由引理5.3.5知，存在一个事件Ω1满足且对任意的ω∈Ω1，存在n1=n1（ω）充分大，使得对所有的n≥n1和任意与[0，1]N相交、边长为的矩形In，都有

对所有的i=1，…，d成立。

设l≥1且

对任意的n≥1，将[0，1]N划分成2nQ个边长为的矩形In，并将包含点x的矩形记为In（x）。对任意的x∈Rl，可以找到满足l≤n≤2l+l0（其中l0仅依赖于N）的最小正整数n使得

从而

其中Vn是满足（6.3.38）式In（x）的并集。显然X（In（x））几乎必然能够被边长为的矩形所覆盖。因此X（In（x））几乎必然能够被个边长为的立方体所覆盖。故

另一方面，[0，1]N\V包含在边长为（这里q=2l+l0）矩形Cqp的并集里，这些矩形中任何一个都不与Rl相交。因此这种矩形的数目至多为

由于X（Cqp）能够被边长为的矩形所覆盖，从而能够被

的立体所覆盖。故当l充分大时，

其中第一和号是对所有边长为rn且与Rl不相交立方体求和。由于可选择l任意大，所以由（6.3.9）和（6.3.40）式可得定理的上界。定理得证。