各向异性随机场轨道性质，引理证明及相关优化

为了确定随机场X像集的确切Hausdorff测度，先给出一些引理。在本章的剩余部分，恒假定0＜H1≤H2≤…≤HN＜1和0＜α1≤α2≤…≤αd≤1，值得注意的是，这两个假定是非本质的，仅仅是为了符号上的方便。设ψ是一个单调非降函数，满足ψ（0+）=0和坐标伸缩性质（见6.2.20）。对任意的上Borel测度μ，定义μ在处的上ψ密度如下：

下面的引理取自Roger（1970）。该引理用于确定Hausdorff测度ψm（E）的下界。

引理6.3.2　设ψ是一非降函数，且满足ψ（0+）=0和坐标伸缩性质，则存在一个正的常数K，使得对任意的上Borel测度μ，以及每个Borel集都有

引理6.3.3　设是一（N，d）-高斯随机场，且满足条件（C2）。则对所有的1≤i≤d，以及任意的存在一个常数c6，3，4＞0使得

证明　令并定义上的一个伪度量

则由条件（C2）可得

且

通过基本的计算可得

如果则由Talagrand（1995）的引理2.1知

因此

对任意的0＜a＜b＜∞，记

其中W（·）表示上的高斯随机测度（见（6.1.3）式）。

引理6.3.4　对所有的1≤i≤d和任意的0＜a＜b＜∞，0＜∈＜rαi，存在一个仅依赖于d和Q的正常数c6，3，5使得

证明　令S={t：ρ（0，t）≤r}并定义上的一个伪度量

则由Yi（a，b，t）的定义和条件（C2）知，对任意的s，t∈I，有

进一步地有，

如果记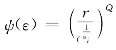，则存在正常数c6，3，6，c6，3，7使得

因此由Talagrand（1995）的引理2.1知，

下面给出本小节的主要引理。证明方法是基于Talagrand（1995）命题4.1的证明思想。

引理6.3.5　存在常数δ1＞0，c6，3，8＞0使得对任意的0＜r0＜δ1，有

证明　设U＞e是一常数，其值后面确定。令rk=r0U-2k，k0=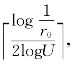则对任意的k≤k0有

因此只需证明

设i=1，…，d，k=0，1，…，令显然对任意的i=1，…，d，k=0，1，…，{Yik}是相互独立的。由引理6.3.4，存在一个正常数c6，3，9使得对任意充分小的r0和任意的k≥0，有(www.xing528.com)

对所有的i=1，…，d，可以选择常数c6，3，9满足故

再由{Yik}的独立性知，

对每个i=1，…，d，记下面证明对任意的i=1，…，d和有

为了证明（6.3.10）式，令S={t∈I：ρ（0，t）≤rk}，并定义上的一个伪度量

则经过一些初等计算和条件（C2），可得对任意的s，t∈I有

更进一步地有，

下面先考虑S在度量di下的直径D。因为

所以只要确定的上界即可。注意到

其中Δi是Yi的谱测度。为了方便，将上式两个积分分别记

由Luan和Xiao（2012）的引理3.5（ii）有

再由Luan和Xiao（2012）的引理3.5（i）可得

联合（6.3.11）—（6.3.14）式可得，

故经过一些简单的计算，有

因此对任意的i=1，…，d，以及可得

令则对充分小的r0＞0，可得

对每个i=1，…，d，令并利用（6.3.15）式，可得

由此及（6.3.9）式可得，

其中最后一个不等式是基于如下的一些事实：r0充分小，以及α1≤α2≤…≤αd和βd≤βd-1≤…≤β1。注意到k0=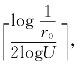当r0充分小时，有

因此可选择充分小的r0使得

联合（6.3.17）和（6.3.18）式可得，

引理得证。