欧氏度量下的维数结果揭示各向异性随机场的样本轨道性质

由于闭区间的结构要比Borel集的结构简单得多，所以本节考虑闭区间在欧氏度量下的维数结果，由此可以看到，所得的结果与上一节在度量τ和ρ下的维数结果有很大的不同。而且我们也没有办法直接在这两类结果之间进行转换。最后值得一提的是，在度量τ和ρ下的维数结果形式要比在欧氏度量下的维数结果简单得多，这在某种意义上意味着度量τ和ρ能够很好的适应随机场的各向异性性。

到目前为止，像集和图集的Hausdorff维数和填充维数都是分别对时间各向异性随机场或空间各向异性随机场单独考虑的，本书所考虑的维数结果是针对时间和空间都是各向异性的随机场，对该问题，目前还没有人进行这方面的研究。下面的定理是关于时空各向异性高斯随机场在闭区间上像集和图集的Hausdorff维数和填充维数结果。

定理5.4.1　设是一个值高斯随机场，且在I=[0，1]N上满足条件（C1）和（C2）。则，以概率1有，

和

其中

证明　首先可以直接验证（5.4.1）和（5.4.2）式中的第三个等式是成立的（见Xiao（1995）中的引理2.3和Xiao（2009）中的引理6.2）。为了证明定理其余的结论，由（1.2.19）式，只需证明图集的上盒维数的上界，像集和图集的Hausdorff维数下界成立。

上界的证明　由于dimHX（[0，1]N）≤d，dimHX（[0，1]N）≤dimHGrX（[0，1]N），所以只需要证明（5.4.2）式的上界。对任意的n≥2，将[0，1]N划分成mn个边长为的子矩形{Rn，i}，则

显然由（5.3.19）式有

从而X（Rn，i）能够被边长为的一个矩形Cn，i所覆盖。因此对每个固定的1≤i≤d，Rn，i×Cn，i能够被mn，l=个边长为的立方体Cn，i，j所覆盖。故对每个1≤l≤d，有

又因为ε＞0是任意给定的，所以

这就证明了

另一方面，对每个固定的1≤k≤N，Rn，i×Cn，i能够被mn，k个边长为cn-1/Hk的立方体所覆盖（其中mn，k=从而

又因为ε＞0是任意给定的，所以

这就证明了

联合（5.4.7）和（5.4.10）式立得（5.4.2）式的上界。

下界的证明　首先证明（5.4.1）式的下界。对任意的0＜γ＜

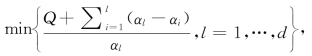只需证明设μX是在映射t↦X（t）下，[0，1]N上Lebesgue测度的像测度，则测度μX的阶为γ的势能为

令

如果存在一个整数1≤l≤d使得则κ=且l-1＜κ≤l。因此由Frostman引理，只需证明：对任意的l-1＜γ＜κ，有

为了估计（5.4.12）中的积分，我们将借助于文献Xiao（1995）中关于处理维数结果的思想来求解。因为X1，…，Xd都是高斯随机变量且相互独立，所以标准化变量独立同分布于标准正态分布N（0，1），其中因此

其中注意到

其中c5，4，1，c5，4，2和c5，4，3是仅依赖于γ的常数。由（5.4.14）式，当对（5.4.13）式的最后一个多重积分关于x1先求定积分时，可得（5.4.13）的最后一个表达式小于

从而分别对dx2，…，dxk-1用类似的讨论，可得（5.4.16）式小于

由γ＜κ有

因为对任意的ε＞0，有

所以由此及（5.4.18）式有

另一方面时，当d-1＜γ＜d时，相似的讨论可得到相同的结果。这就证明了（5.4.1）式的下界。

下面转向证明（5.4.2）式的下界。如果Q≤Λ，则由（5.4.1）和（5.4.7）式，可得

如果Q＞Λ，则dimHX（[0，1]N）=d。因此

令λ=如果存在一个整数k使得显然有d+N-k＜λ≤d+N-k+1。为了证明（5.4.2）式的下界，只需证明：对任意的0＜γ＜λ有，

采用与（5.4.12）式类似的讨论可得(www.xing528.com)

因为所以由文献Xiao（2009）中的引理6.4和一些简单的计算，可得（5.4.20）式是成立的。这就完成了对（5.4.2）式下界的证明。故定理5.4.1得证。

下面的结论是关于水平集的Hausdorff维数和填充维数结果。

定理5.4.2　设值高斯随机场，且在I=[0，1]N上满足条件（C1）和（C2）。如果Q＞Λ，则对每个在一个正概率事件集上有

证明　首先证明上界，证明方法类似于Xiao（2009）关于水平集维数的讨论。将划分成2nQ个边长为的矩形Bn，q。如果x∈X（Bn，q），则令En，q=Bn，q，否则令En，q=∅。显然，对给定的n，En，q全体构成Lx的一个覆盖。由（1.2.19）式，只需证明

事实上，对每个k∈{1，2，…，N}，En，q能够被个边长为

的立方体所覆盖。从而Lx能够被Mn，k个边长的立方体所覆盖。注意，Mn，k显然是一个随机变量，下面计算Mn，k数学期望。

给定δ∈（0，1），令tn，q是矩形En，q的左下角点，则由文献Talagrand（1995）的引理2.1和一些初等计算后有，

由（5.4.24）式知，

令则由（5.4.25）式，Markov不等式和Borel-Cantelli引理知，当n充分大时，Mn，k≤c2nηa.s.。从而

令δ沿着有理数趋于0，则

又因为k∈{1，2，…，N}是任意给定的，所以对（5.4.26）式两边取最小值可得（5.4.23）式，即

这就完成上界的证明。

下面证明下界。设则

将上式的右边记为γ。剩下的只需证明：存在常数c5，4，4＞0使得

为了证明（5.4.27）式，我们将基于文献Xiao（2009）中定理7.1的证明方法。先构造一列Borel集上的随机正测度σn如下：

设是测度σn的γ-势能，即

如果能证明存在有限正的常数c5，4，5，c5，4，6和c5，4，7使得

则（5.4.27）式成立且c5，4，4=

下面验证（5.4.30）和（5.4.31）式。由于X的各个分量是相互独立的，所以由Fubini定理有，

其中这就证明了（5.4.30）式中的第一个不等式。

下面证明（5.4.30）式中的第二个不等式。再次利用X各个分量的独立性和Fubini定理，可得

其中Γl（s，t）=Var（Xl（s））·Var（Xl（t）｜Xl（s））和条件（C3）有，

由此和（5.4.32）式知，

其中最后一个不等式由条件Λ＜Q可得。

与（5.4.32）类似地可以得到，

因为对任意的所以

又由于γ=所以

由此和（5.4.33）式可得，

这就证明了（5.4.32）式，从而定理5.4.2得证。