各向异性随机场样本轨道的Hausdorff维数

为了确定像集的Hausdorff维度，我们需要下面的引理，该引理给出了时空各向异性高斯随机场的一致连续模。

引理5.3.5　设是一个零均值，值高斯随机场，且满足条件（C2）。则以概率1存在一个依赖于N，H和α的随机变量A使得A具有有限的任意阶矩，以及对任意的d，有

证明　引理的证明是基于Xiao（2009）中对定理4.2的证明方法。利用众所周知的Garsia-Rodemich-Rumsey连续性引理的拓展形式（见Xiao（2009）的定理4.1），然后选择Garsia-Rodemich-Rumsey连续性引理中所用的两个具体函数和p（x）=，其中c5，1，2＞0是（5.1.2）式中的常数，就可以得到定理的结论。

有了前面的准备后，可以得到关于像集Hausdorff维数的定理如下：

定理5.3.6　设是一个值高斯随机场，且满足条件（C1）和（C2），则对任意的Borel集以概率1有，

证明　将定理的证明分成两部分，一部分利用覆盖讨论方法证明上界，另一部分利用容度讨论方法证明下界。

首先证明上界。因为所以由（4.2.3）式知

因此对于上界，只需证明由Hausdorff维数的σ-稳定性，不妨假设利用Hausdorff测度的定义可得，对任意的γ＞和δ＞0，存在E的一列半径为rj的开球{Bρ（uj，rj）}覆盖，使得rj≤δ且由引理5.3.5知，对任意的ε＞0，存在一个具有有限阶矩的随机变量A使得对所有的i∈{1，…，d}有

由此可得

因此在度量τ下，每个X（Bρ（uj，rj））可由一个半径为的球所覆盖。由此以及有，X（E）可由一列半径为的τ-球所覆盖。由于

所以

又因为ε＞0和γ＞是任意给定的，所以

这就证明了定理5.3.6的上界。(www.xing528.com)

下面证明下界。为了证明下界，只需证明：对任意

因为所以由Frostman引理，存在E上的一个概率测度σ使得

设μ是在映射t↦X（t）下的像测度，则μ是X（E）上的一个概率测度。为了证明只需证明

为此，注意到

又因为X1，…，Xd是独立同分布的高斯随机变量，所以它们的标准化变量独立同分布于标准正态分布N（0，1），其中因此

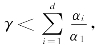其中第二个等式由条件（C2）可得。由于所以

故联合（5.3.24）—（5.3.26}）式，可得其中最后一个不等式由（5.3.22）式可得。从而（5.3.23）式几乎必然成立。这就完成了定理5.3.6的证明。

注5.3.7　下面是关于像集和逆向集结论的两点注。

（i）由定理5.3.6有，在度量τ下像集X（[0，1]N）的Hausdorff维数为

（ii）虽然本文获得了在度量τ和ρ下像集和逆向集的Hausdorff维数，但是到目前为止，我们还没找到有效的方法来确定在度量τ和ρ下图集的

Hausdorff维数。