时空各向异性高斯场碰撞概率的上下界

本节主要研究如（5.1.1）式所定义的时空各向异性高斯随机场的碰撞概率。首先对一些符号进行说明，并给出几个引理，然后给出本节的主要结论-定理5.2.5并给予证明。

为了研究时空各向异性高斯随机场的碰撞概率和维数结果，将在空间上引入度量τ来克服空间变量所带来的各向异性性，定义如下：

其中x=（x1，…，xd），y=（y1，…，yd）∈

由§1.2的第三部分，在度量空间上可以定义β-维Hausdorff测度（β＞0）和Hausdorff维数，分别记还可以定义在度量τ下牛顿β-势和牛顿β-容度，分别记为同理可以定义在度量空间上对应的β-维Hausdorff测度（β＞0）、Hausdorff维数、在度量ρ下牛顿β-势和牛顿β-容度，分别记为

为了证明关键性引理5.2.3，需要用到下面两个引理。

引理5.2.1　设d是一个正整数，β≥1，以及对所有的1≤i≤d有ai≥0，则存在一个不依赖于ai（1≤i≤d）的正整数c5，2，1使得

证明　通过基本的方法可以证明结论对d=2是成立的。对于一般的情况由数学归纳法可证。

引理5.2.2　设d是一个正整数，β≥1，1≤β1≤β2≤…≤βd＜∞，以及对所有的1≤i≤d，有ai≥0。则

（i）如果对所有的1≤i≤d，有ai≤1，则存在一个不依赖于ai（1≤i≤d）的正常数c5，2，2使得

（ii）如果至少存在一个i∈{1，2，…，d}使得ai≥1，则存在一个不依赖于ai（1≤i≤d）的正常数c5，2，3使得

证明　（i）因为1≤β1≤β2≤…≤βd，以及对所有的1≤i≤d有ai≤1，所以存在正的常数c5，2，2使得

其中最后一个不等式由引理5.2.1可得。

（ii）分两种情形进行讨论。

情形1　如果对所有的1≤i≤d有ai≥1，则利用引理5.2.1和1≤β1≤β2≤…≤βd可得，存在正常数c使得

情形2　如果恰好存在{1，2，…，d}中的p（1≤p＜d）个数k1，…，kp使得aki≥1（1≤i≤p），则存在{1，…，d}上的一个置换σ使得σ（i）=ki（1≤i≤p）。令β*=min{βσ（1），…，βσ（p）}。由引理5.2.1有

其中最后一个不等式由β1=min{β*，βσ（p+1），…，βσ（d）}和可得。现在用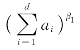去除（5.2.6）式的两边有，

其中第二个不等式由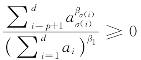可得，最后一个不等式是因为所有联合（5.2.6）和（5.2.7}）式，可得这就完成引理5.2.2的证明。

下面是本节的两个关键性引理。它们的证明方法是基于Biermé等人（2009）的论证方法。

引理5.2.3　设X=是一个值高斯随机场，且满足条件（C1）—（C3），则存在常数c5，2，4＞0使得对任意的

I，有

其中Γn（s，t）=+Cov（X（s），X（t））。

证明　因为X1，…，Xd是相互独立的，所以

其中Φni（s，t）=+Cov（Xi（s），Xi（t））。又因为Φni（s，t）是正定的，所以

其中det（Φni（s，t））表示Φni（s，t）的行列式。注意到

并利用条件（C2），（C3），以及Biermé等人（2009）对其文中（3.12）式的讨论方法，可得对任意的s，t∈I和有

其中c是一仅依赖于I的正常数。

联合（5.2.9）—（5.2.12）式有

利用条件（C3）和不等式det（A+B）≥det（B）（这里A和B是两个正定矩阵），可得

当对所有的i∈{1，2，…，d}有ai≥0时，不等式显然成立，从而有

下面分3种情况讨论：

情形1　且对所有的1≤i≤d，有

由（5.2.15）式和引理5.2.3的第一部分有

因此由不等可得（5.2.13）式的右边表达式是小于或等于

从而利用（5.2.14）式，可得（5.2.17）式的右边表达式小于或等于

故由（5.2.13）、（5.2.17）和（5.2.18）式，可得

情形2　且至少存在一个i∈{1，2，…，d}使得

由（5.2.15）式和引理5.2.3的第二部分有

因此由不等式可得（5.2.13）式的右边表达式是小于或等于

从而利用（5.2.14）式，可得（5.2.21）式的右边表达式小于或等于

故由（5.2.13）、（5.2.21）和（5.2.22）式，可得

情形3　

显然（5.2.13）式的右边表达式是小于或等于

再次利用（5.2.14）式，可得（5.2.24）式小于或等于

因此由（5.2.13）、（5.2.24）和（5.2.25）式有

联合（5.2.19）、（5.2.23）和（5.2.26）式，可得

这就完成了引理5.2.3的证明。

下面引理是Biermé等人（2009）引理3.1的推广。

引理5.2.4　设是一个值高斯随机场，且满足条件（C1）—（C3），则对任意的M＞0，存在正常数c5，2，5和δ0使得对任意的r∈（0，δ0），s∈I和x∈[-M，M]d，有(www.xing528.com)

证明　因为X的各个分量过程是相互独立的，而且

所以只需估计事件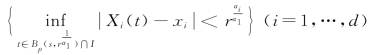的概率。由高斯分布的条件期望公式有

注意到对任意的t∈I，高斯随机变量Xi（t）-ci（s，t）Xi（s）和Xi（s）是相互独立的，从而利用三角不等式，可推得

其中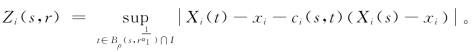由条件（C2）和Cauchy-chwarz不等式有

因此从（5.2.31）式可推得，存在正的常数δ0使得对任意的r∈（0，δ0）和t有1/2≤ci（s，t）≤3/2。再利用零均值高斯场的单峰性可得

由于Zi（s，r）和ci（s，t）Xi（s）是相互独立的，所以由（5.2.30）式可得

下面估计则Yi（t）是一高斯场且Yi（s）=0。可定义Yi（t）的标准度量

在经过基本的计算后可得到

和

其中的度量熵。

利用Dudley定理有

其中最后一个不等式由变量替换可得。现将上式中最后一个积分划分成两部分，则

首先估计K2。显然有

下面估计K1。利用分部积分公式和变量替换，可得

由（5.2.34）—（5.2.37）有

联合（5.2.30），（5.2.32），（5.2.33）和（5.2.38）式，可得

由于X的各个分量过程是相互独立的，所以（5.2.32）式成立。引理5.2.4得证。

下面的定理是本章的主要结论，该结论给出了时空各向异性高斯场碰撞概率的上下界，其中上下界分别由度量τ下的Hausdorff测度和容度表示。

定理5.2.5　设X=是一个值高斯随机场，且满足条件（C1）—（C3）。当Λ＞Q，M＞0时，则存在正常数c5，2，6，c5，2，7使得对任意的Borel集F⊆[-M，M]d，有

其

证明　证明方法是基于Xiao（2009）定理7.6的证明思想。首先证明上界。不妨设

否则结论显然成立，从而可以选择并固定一个任意常数由Hausdorff测度的定义知，存在一列半径rj＜δ0（δ0同引理5.2.4中定义）的开球使得

显然有

对每个j≥1，可将立方体I划分成个边长为的矩形，从而在度量ρ下，I可由至多个半径为的球所覆盖。故由引理5.2.4有

联合（5.2.41）和（5.2.42）式，可得

又因为是任意给定的常数，所以上界得证。

下面证明碰撞概率的下界。不妨设否则结论显然成立。由容度的定义（见§1.2）知，存在使得

定义I上的一列随机测度如下：

令是测度νn的总质量，即下面证明

其中正的常数c5，2，8，c5，2，9不依赖于n和μ。由于Xi，i=1，…，d是相互独立的，所以

其中这就证明了（5.2.46）式中的第一个不等式。

下面证明（5.2.46）式中的第二个不等式。注意到

dξdημ（dx）μ（dy）dsdt。

从而由引理5.2.3有

接下来将（5.2.48）式中定积分的积分区域划分为

和并将在它们上面的定积分分别表示显然有

其中最后一个不等式利用到如下的事实：对每个s∈I，集合是包含在一个边长为的矩形中。另一方面，

其中最后一个不等式利用到极坐标下的变量替换，并注意到ρ（0，t）是一齐次函数（见Biermé等人（2007））。联合（5.2.48）—（5.2.50）式，可得

这就证明了（5.2.46）式中的第二个不等式（5.2.46）。因此，利用Kahane（1985）的方法，可以证明如下事实：存在一个支撑集在X-1（F）∩I上的有限正测度ν使得νn弱收敛于ν，且

这就完成了碰撞概率下界的证明，从而定理得证。

从定理5.2.5可以得到下面的推论，该推论给出了X（t）能够击中一个Borel集的充分条件。

推论5.2.6　设X=是一个值高斯随机场，且满足条件（C1）—（C3）。当Θ：=时，则对任意的Borel集下面的结论成立：

（i）如果

（ii）如果

注5.2.7　当令α1=α2=…=αd=1时，由本文的结论可得Xiao（2009）的结论。事实上，设X=是一个值高斯随机场，且满足条件（C1）—（C3）。当α1=α2=…=αd=1，d＞Q，M＞0时，则存在常数c5，2，10，c5，2，11＞0使得对任意的Borel集F⊆[-M，M]d，有

如果α1=α2=…=αd＜1，则（5.2.52）式等价于

其中c5，2，12和c5，2，13是两个正常数。关于这点，可参看Ni和Chen（2016）的例4.1或本书例2.4.1。