两个随机场空间集的相交性各向异性随机场样本轨道性质

令Y（s，t）=（XH（s），XK（t）），s∈，则事件与事件等价，其中为了研究随机场XH和XK的相交性，采用与（3.2.9）式类似的方式定义上的一个新的度。从而可以定义新度量下的Hausdorff测度

用表示球心在（s，t，x），半径为r的球。显然有

其中分别如（3.2.5）和（3.2.6）式所定义。

设分别是空间上的两个度量，定义为

对任意的实数β1和β2，考虑势核定义为

其中fα是由（1.2.30）式所定义。从而可以在度量空间上定义关于关于势核的（β1，β2）-容度，记为

用h1表示在度量下矩形I1的直径，即用h2表示在度量下矩形I2的直径，即设势核κν：定义为

其

可以用类似上节关于能和容度的定义方法，给出关于势核κν的能和容度，分别记为

同理，用

表示Borel集的φQ-Hausdorff测度，其中φQ（s）：=（当2d＞Q时，φQ（s）显然在原点附近是右连续的和非降的函数，且

下面的定理是本节的主要结论。该定理回答了当把“时间”s，t分别限定在E1和E2时，在何种情况下XH和XK会在F中相交，其中F是上的一Borel集。

定理3.4.1　设X=和X=是

如（3.2.1）和（3.2.2）式所定义的两个高斯随机场。对任意的Borel集E1存在仅依赖于I1，I2，H和K的常数c3，4，1，c3，4，2＞0使得

证明　证明方法是基于Xiao（2009）定理7.6的证明思想。先证明（3.4.5）式的上界。不妨，否则结论显然成立。因此可以选择并固定一个任意常数从而存在中的一列球使得

显然有

又因为随机场XH和XK相互独立，所以由引理2.2.3有，

联合（3.4.6）和（3.4.7）式，可得

因为是任意给定的，所以上界得证。

下面证明下界。不妨设Cd，d（E1×E2×F）＞0，否则结论显然成立。由Choquet容度定理（见Khoshnevisan（2002）），可以假设F是一紧集，且存在常数M＞0使得

由容度的定义知，存在使得

考虑E1×E2×F上的一随机测度列定义为

用表示测度νn的总质量，即先证明下面两个不等式成立：

其中正常数c3，4，3，c3，4，4仅依赖于n和μ。

首先，由（3.4.10），Fubini定理和XH与XK的独立性知，

这就证明了（3.4.11）式中的第一个表达式。

下面证明（3.4.11）式中的第二个表达式。令

并用（ξ，ξ′）T表示行向量（ξ，ξ′）的转置。

由（3.4.10），Fubini定理和XH与XK的独立性知，

将上述积分的积分区域划分成D1，D2，D3和D4，并将在它们上面的积分分别表示为(https://www.xing528.com)

这里

由引理2.2.4知，如果（（s，t，x），（s′，t′，x′））∈D1，则

其中如果（（s，t，x），（s′，t′，x′））∈D2，则

注意到

由Cauchy-Schwarz不等式，函数在

I上非负且连续。又因为所以该函数仅在t=t′时为0。

因此，对任意的（（s，t，x），（s′，t′，x′））∈D2，det（ΓK，n（t，t′））≥c。故

因为存在正常数c3，4，5，c3，4，6使得所以此外，显然

同理，可以证都是小于等于由此及（3.4.13），（3.4.14），（3.4.15）式，可得

因此，利用Kahane（1985）所采用的方法可以得到，存在支撑集在上的一有限正测度使得以及

故下界得证。从而定理证毕。

通过令E1=I1，E2=I2，则可以得到下面的推论。

推论3.4.2　在定理3.4.1的条件下，如果d≥Q，则存在仅依赖于I1，I2，H和K的常数c3，4，7，c3，4，8＞0使得

证明　证明方法是基于Chen和Xiao（2012）推论2.2的证明思想。由Choquet容度定理（见Khoshnevisan（2002）），可以假设F是一紧集，且存在常数M＞0使得利用定理3.4.1，只需要证明对任意的区间I1和I2（由（2.2.4）式定义），存在正的有限常数c3，4，9和c3，4，10使得对任意的Borel集有

和

首先证明（3.4.19）式。令N=N1+N2，设是一个任意常数，则存在一列球使得

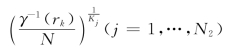对每个k≥1，将矩形I1划分个边长为的立体Ck，m，也将矩形I2划分为个边长为的立体Ck，l，从而

这就得到了在度量下I1×I2×F半径为rk的球覆盖。因此

其中Q=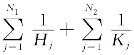如节3.2所定义。这就证明了（3.4.19）式。

下面证明（3.4.20）式。不妨设否则结论显然成立。对任意的存在F上的一个概率测度σ使得

设λ1和λ2分别是I1和I2上的规范Lebesgue测度（即均匀测度），并令μ=λ1×λ2×σ，则μ是I1×I2×F上的一个概率测度。从而只需证明

又因为

所有只需证明

但是（3.4.22）和（3.4.23）式可通过采用与（2.3.24）式同样的方法进行验证。从而推论3.4.2得证。

推论3.4.3　在定理3.4.1的条件下，有下面的结论成立。

（i）如果函数都在原点附近可积，则

（ii）如果当r→0时，有且函数φQ（s）=在原点附近单调非减，以及§2.2条件（C1）和（C2）成立，则

证明　因为随机场是相互独立的，且满足条件A和B，因此推论3.4.3可由推论3.3.3的方法证明。