两个随机场相交性研究

设XH和XK分别由（3.2.1）和（3.2.2）定义的高斯随机场。进一步地假设两个随机场XH和XK是相互独立的。

下面的定理回答了问题（i）所提出的问题，即将“时间”s，t分别限定在E1和E2时，确定了在何种情况下，XH和XK会相交。

定理3.3.1　设X={XH（s），s∈}和X={XK（t），t∈}分别是由（3.2.1）和（3.2.2）定义的两个独立高斯随机场。则对任意的两个Borel集E1⊆I1和E2⊆I2，存在仅依赖于I1，I2，H和K的常数c3，3，1，c3，3，2＞0使得

证明　证明方法是基于Chen和Xiao（2012）定理3.1的证明思想。设Z（s，t）=XH（s）-XK（t），s∈则事件{XH（E1）∩XK（E2）等价于事件注意到F={0}是一有界Borel集，如果可以证明以下两个结论：

（2）存在正常数δ0和c3，3，4使得对满足的任意（s，t），（s′，t′）∈I，有

其中Z（s，t）的各个分量独立同分布于Z0（s，t）。则由定理2.3.1知，这个式子与（3.3.1）式等价，从而定理得证。

下面证明（3.3.2）和（3.3.3）式成立。事实上，由Z0（s，t）的定义和XH与XK的独立性知，

因为γ（r）是一上凸函数，所以

其中第一个不等式由（3.2.3）和（3.2.4）式可得，第二个不等式由如下基本不等式可得：

又因为γ（r）是严格递增函数，所以

另一方面，再次利用（3.2.3）和（3.2.4）式，以及引理3.2.1，可得

联合（3.3.6）和（3.3.7）式，可得（3.3.2）式，从而（3.3.2）式成立。

下面证明（3.3.3）式。对任意的（s，t），（s′，t′）∈I，利用两个随机场的独立性知，

当时，由条件B和（3.3.8）式，有

其中第二个不等式由如下基本不等式可得：(https://www.xing528.com)

而第三个不等式由引理3.2.1可得。令δ0=δ，则当δ0时，有（3.3.9）式成立。这就证明了（3.3.3）式。故定理3.3.1得证。

下面考虑定理3.3.1的特殊情形。用表示在度量下矩形I的直径，即

设势核κν：定义为

其中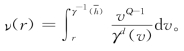由§1.2节第3部分，可以定义关于势核κν的牛顿能和牛顿容度，分别记为。令φQ（s）：=则当d≥Q时，φQ（s）在原点附近是右连续的和非增函数，且对函数φQ（s），由§1.2节第3部分，可以定义φQ（s）-Hausdorff测度，记为

令E1=I1，E2=I2，则有下面的推论。

推论3.3.2　在定理3.3.1的条件下，如果d≥Q，则存在仅依赖于I1，I2，H和K的常数c3，3，5，c3，3，6＞0使得

证明　设Z（s，t）=XH（s）-XK（t），s∈则事件和事件是等价的。因为Z（s，t）的各个分量独立同分布于Z0（s，t），且Z0（s，t）满足（3.3.2）和（3.3.3）式，所以由推论2.3.2，可以证明从而（3.3.11）式成立。

推论3.3.3　在定理3.3.1的条件下，则有下面的结论成立。

（i）如果函原点附近可积，则

（ii）如果当r→0时，有且函数在原点附近单调非减，以及§2.2条件（C2）成立，则

证明　（i）如果函数在原点附近可积，则从而有因此结论成立。

（ii）因为γ（r）是连续的、严格单调增的函数，所以它的逆函数γ-1（r）存在，且令r=γ-1（s），则与sd=o（（γ-1（s））Q）等价，因此

联合（3.3.13），φQ-Hausdorff测度的定义和B（x，∈）是{x}的一个覆盖，可得

故由推论3.3.2知因此结论得证。