在本节中,将利用Bernstein理论和Estrade等人(2011)的方法构造由(2.2.2)定义的高斯随机场,该随机场具有平稳增量,且满足γ(x)=xαL(x),其中α∈[0,1)是一个常数,L(x)在x=0处是规则慢变的非负函数。从Xiao(2009)或Xue和Xiao(2011)的文中可得,存在许多具有平稳增量的高斯场例子,且这些高斯场的增量二阶矩与ρ2(s,t)是可比的,即存在具有平稳增量的高斯场满足
其 因此,由Estrade等人(2011)中的命题2.1知,只要能够构造出一类Bernstein函数φ满足
因此,由Estrade等人(2011)中的命题2.1知,只要能够构造出一类Bernstein函数φ满足
则可得到所要构造的例子。
由Schilling等人(2012)定理3.2可知,对任一Bernstein函数φ可表示为
其中a≥0,b≥0,ν是(0,∞)上的Lévy测度并满足
令a=b=0,并选择Lévy测度ν满足
其中α∈[0,1)是一个常数,L是在0附近规则慢变化的函数。为此,由Fubini定理有,
因为当x→0+时,φ(x)的渐近行为是由ν([t,∞))在t→∞时的渐近行为确定的,所以我们将令
其中α∈[0,1)是一个常数,l(t)是在无穷远附近规则慢变化的函数。可以证明ν是一个Lévy测度(这由Schilling等人(2012)的注3.3(iii)可得)。
如果α=0,则由(2.4.1)式有,
利用变量替换可得
又由控制收敛定理知
因此有
作为例子,如果令α∈(0,1),l(1/x)=1,则存在具有平稳增量的零均值高斯随机场X0满足X0(0)=0和
其中φ(x)=xα。即γ(r)=![]() 显然,γ(r)满足2.2中关于γ(r)的所有条件。因此可得到第一个例子,与该例子相关的结论可见Xiao(2009)和Biermié等人(2009)。
显然,γ(r)满足2.2中关于γ(r)的所有条件。因此可得到第一个例子,与该例子相关的结论可见Xiao(2009)和Biermié等人(2009)。
例2.4.1 设X=![]() 是由(2.2.2)所定义的
是由(2.2.2)所定义的![]() 值高斯随机场。如果0<H1,H2,…,HN<1,γ(r)=rα(0<α<1)和d≥
值高斯随机场。如果0<H1,H2,…,HN<1,γ(r)=rα(0<α<1)和d≥![]()
![]() 则对Rd中任意的Borel集F,存在常数c2,4,3,c2,4,4>0使得
则对Rd中任意的Borel集F,存在常数c2,4,3,c2,4,4>0使得
如果令α∈(0,1),l(1/x)=![]() 则存在具有平稳增量的零均值高斯随机场X0满足X0(0)=0和
则存在具有平稳增量的零均值高斯随机场X0满足X0(0)=0和
其中φ(x)=![]() 因为证明中主要只涉及γ(r)在原点附近的情况,所以从现在起我们将假设r∈[0,1)。因此γ(r)=
因为证明中主要只涉及γ(r)在原点附近的情况,所以从现在起我们将假设r∈[0,1)。因此γ(r)=![]()
![]() 故有
故有
例2.4.2 设X=![]() 是由(2.2.2)所定义的
是由(2.2.2)所定义的![]() 值高斯随机场。如果H∈(0,1)N,γ(r)=rαlogβ(1/r),0<α<1,β∈R。则下面的结论成立:
值高斯随机场。如果H∈(0,1)N,γ(r)=rαlogβ(1/r),0<α<1,β∈R。则下面的结论成立:
(i)若d>![]() 则对
则对![]() 中任意的Borel集F,存在常数c2,4,5,c2,4,6>0使得
中任意的Borel集F,存在常数c2,4,5,c2,4,6>0使得
其中φ(s)=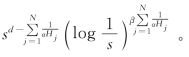 (https://www.xing528.com)
(https://www.xing528.com)
(ii)若d= 则对
则对![]() 中任意的Borel集F,存在常数c2,4,7>0使得
中任意的Borel集F,存在常数c2,4,7>0使得
其中φ(s)=![]()
(iii)若d=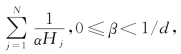 则对
则对![]() 中任意的Borel集F,存在常数c2,4,9>0使得
中任意的Borel集F,存在常数c2,4,9>0使得
其中Kν(s)=![]()
(iv)若d=![]() ,则(2.4.5)式中的下界在Kν(s)=1时成立。
,则(2.4.5)式中的下界在Kν(s)=1时成立。
(v)若d< 则(2.4.5)式中的下界在Kν(s)=1时成立。
则(2.4.5)式中的下界在Kν(s)=1时成立。
注2.4.3 在结论(iii)—(v)中,由于![]() 所以φ(s)不是一个规范函数。因此用本文的方法无法得到碰撞概率的上界。但是由结论(iii)—(v)知,当d=
所以φ(s)不是一个规范函数。因此用本文的方法无法得到碰撞概率的上界。但是由结论(iii)—(v)知,当d= 且β≥0或d<
且β≥0或d< 时,X以正的概率击中F。
时,X以正的概率击中F。
证明 (i)与Nualart和Viens(2013)的命题4.7类似地可证明:如果极![]() 存在,则函数K和1/φ是相当的当且仅当d>
存在,则函数K和1/φ是相当的当且仅当d>![]()
![]() 如果能够验证γ(r)是连续的,严格递增的和向上凸的,且满足条件(C2)、(C3)和d>Q/
如果能够验证γ(r)是连续的,严格递增的和向上凸的,且满足条件(C2)、(C3)和d>Q/![]() 则结论成立。而γ(r)的这些性质可用Nualart和Viens(2013)的论证方式加以验证。
则结论成立。而γ(r)的这些性质可用Nualart和Viens(2013)的论证方式加以验证。
(ii)—(v)证明与Nualart和Viens(2013)的命题4.7类似,此处略去。
最后,令α=0,l(1/x)=![]() 则存在具有平稳增量的零均值高斯随机场X0满足X0(0)=0和
则存在具有平稳增量的零均值高斯随机场X0满足X0(0)=0和
其中![]() 也就是,
也就是,![]() 因此得到下面的例子。
因此得到下面的例子。
例2.4.4 设X=![]() 是由(2.2.2)所定义的
是由(2.2.2)所定义的![]() 值高斯随机场。如果d>Q,γ(r)=log-β(1/r),β>1/2,则对Rd中任意的Borel集F,存在常数c2,4,10>0使得
值高斯随机场。如果d>Q,γ(r)=log-β(1/r),β>1/2,则对Rd中任意的Borel集F,存在常数c2,4,10>0使得
其中Kν(s)=1。
证明 如果能够验证γ(r)满足§2.2中关于γ(r)的所有条件,则由推论2.3.2知结论成立。
显然γ(r)在(0,1)上是一个连续的、严格递增的和向上凸的函数。因此只需验证γ(r)满足条件(C1)和(C2)。
条件(C1):当0<r,v<e-1时,log(1/r)>1和log(1/v)>1显然成立。因为β>1/2,所以
因此可选择m=c,r0=e-1,则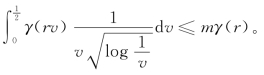
条件(C2):由β>1/2有,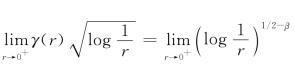 =0。
=0。
因为测度函数
所以只需考虑下界。下面直接计算ν(r)。由于Q-1>0,所以存在M>0,
h1≤h使得对所有的s<h1有sQ-1(log1/s)βQ≤M成立。因此
又因为ν(r)是有界函数。所以ν(γ-1(x))也是有界函数。故可直接令Kν(s)=1。由此结论得证。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




