各向异性随机场样本轨道性质和高斯随机场的定义

定义1.2.1　设）是一个概率空间，。若X（t，ω）：Ω×关可测（这是T上的Borel集全体），则称X（t，ω）为定义在Ω×T上的值随机场，简称（N，d）-随机场。

为了方便，通常用X（t）表示定义在Ω×T上的随机场X（t，ω），即ω常常省略不写。当N=1时，X（t）就是随机过程，而随机场通常是用来强调参数空间的维数N≥2的过程。当固定ω∈Ω时，则称确定性函数X（t，ω）：T为随机场X的样本轨道函数或一次实现，通常简称为样本轨道。本书主要讨论随机场的样本轨道性质。

本书涉及的随机场主要有两大类：高斯随机场和stable随机场。高斯随机场定义如下：

定义1.2.2　高斯随机场是指其任一有限维分布都是多元正态分布，即对任意的n≥1，t1，…，tn∈N，都有（X（t1），…，X（tn））为n元正态随机向量。其特征函数为

其中μ=E（X（t1），…，X（tn））′，Σ是（X（t1），…，X（tn））的协方差阵。

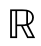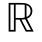由于本书只考虑可调和stable随机场，因此先考虑关于对称的α-stable（简记为SαS）随机测度的随机积分，从而得到可调和stable随机场的定义。设Wα是N上一个由Lebesgue测度控制的各向同性、独立分散的SαS随机测度（具体的定义见Samorodnitsky和Taqqu（1994）第3章和第6章，此处0＜α＜2），而f（t，·）：是定义在N上的复值可测函数且Lα（N）可积。即，

采用与Samorodnitsky和Taqqu（1994）相同的方法，我们定义关于SαS随机测度的随机积分。(www.xing528.com)

定义1.2.3　在条件（1.2.2）下，随机场

有定义，且{Y（t），t∈RN}是一实值各向同性的SαS随机场。

另外，经过适当的规范化处理后（见Samorodnitsky和Taqqu（1994）的定理6.3.1和6.3.4），对任意给定的整数n≥0及s0，…，sn∈RN，随机变量Y（s0），…，Y（sn）联合分布的特征函数由下式给出：

其中所有bj是任意的实数，是上的拟范数，定义为：

因此由（1.2.4）和（1.2.5）有，的尺度参数为