目前研究的各向异性随机场主要分为三大类,其一是时间各向异性随机场,其二是空间各向异性随机场,其三是时间和空间都是各向异性随机场(见Xiao(2013))。下面给出这三类各向异性随机场的具体定义,以及介绍与这三类各向异性随机场随机相关轨道性质的研究情况。
设X={X(t),t∈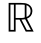 N}是一(N,d)随机场,定义如下:
N}是一(N,d)随机场,定义如下:
其中假定各坐标分量Xi(t)是随机连续的。令
则对每个t∈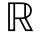 N,有
N,有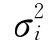 (t,h)→0,
(t,h)→0, →0。
→0。
(1)设X1(t),…,Xd(t)是独立同分布的,且各分量Xi(t)在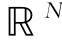 中沿着不同方向变化时,有不同的分布属性,则称X是一时间各向异性随机场。时域算子自相似随机场是时间各向异性随机场一个重要特例。一个(N,d)随机场X称为时域算子自相似随机场是指存在一个N×N矩阵E使得对于所有的常数c>0,都有
中沿着不同方向变化时,有不同的分布属性,则称X是一时间各向异性随机场。时域算子自相似随机场是时间各向异性随机场一个重要特例。一个(N,d)随机场X称为时域算子自相似随机场是指存在一个N×N矩阵E使得对于所有的常数c>0,都有
其中符号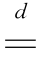 表示(1.1.3)式左右两边随机场有相同的有限维分布,而cE是
表示(1.1.3)式左右两边随机场有相同的有限维分布,而cE是 上的算子定义为:
上的算子定义为:
(1.1.3)式表明当X沿着时间的各个方向有不同的变化率时,在空间上却表现出同比例的变化,即时间的各向异性。
分数布朗单是时间各向异性高斯随机场的一个重要例子,该例子是由Kamont(1996)引进的,可以验证分数布朗单是时域算子自相似的。对于分数布朗单的研究已经取得了很多的成果。例如,Ayache等人(2002)给出了分数布朗单的移动平均表示,并研究了轨道的连续性,而Herbin(2006)给出了分数布朗单的调和表示;Dunker(2000),Mason和Shi(2001),Belinski和Linde(2002),Kuhn和Linde(2002)研究了分数布朗单的小球概率;Mason和Shi(2001)计算了与分数布朗单的轨道波动相关例外集的Hausdorff维数;Øksendal和Zhang(2001)和Hu等人(2004)研究了由分数布朗单驱动的随机偏微分方程;Kamont(1996)和Ayache(2004)研究了分数布朗单像集的盒维数和Hausdorff维数;Ayache和Xiao(2005)用小波方法研究了分数布朗单的一致和局部近似属性,并给出了[0,1]区间上像集、图集和水平集的Hausdorff维数;Wu和Xiao(2007)给出了分数布朗单像集的几何性质和Fourier解析性质,其结论体现出时间各向异性与时间各向同性有很大的差异;Xiao和Zhang(2002)研究了分数布朗单局部时的存在性,并给出了局部时联合连续的一个充分条件;Ayache等人(2008)在最优的条件下,建立了局部时的联合连续性,并研究了最大局部时的一致Holder条件。
时间各向异性高斯随机场的例子除了分数布朗单外,还有由时空白噪声驱动的随机热方程的解(见Muller和Tribe(2002),Hu和Nualart(2009))和Xiao(2009)所给出的一般条件下时间各向异性高斯随机场等。Xiao(2009)对其所提出的时间各向异性随机场进行了较完整性的研究,如研究了过程的连续性、一致连续模、小球概率,像集和图集的Hausdorff和packing维数、水平集的Hausdorff维数、碰撞概率和局部时及其联合连续性等。值得一提是,Xue和Xiao(2011)构造了一类时间各向异性高斯随机场,并研究了其轨道性质和最优渐近估计和预测。Ayache和Xiao(2016)考察了一类可调和分数stable场的局部不确定性和局部时的联合连续性。(https://www.xing528.com)
对时间各向异性随机场的研究,已经得到相当多的结果。目前,时间各向异性性由某个正定矩阵确定的随机场正得到越来越多概率学者的关注(见Benon等人(2006),Biermé和Lacaux(2009),Biermé等人(2007),Didier和Pipiras(2011),Li和Xiao(2011),Biermé等人(2017)),关于该随机场的研究也正处于初步阶段。
(2)考虑X的各个分量Xi(t)对应的σi(t,h),当 →0时,σi(t,h)有不同的变化率,则称X是空间各向异性随机场。与时间各向异性高斯场类似,空间各向异性随机场也有空域算子自相似高斯随机场,定义为:存在一个d×d矩阵D使得对于所有的常数c>0,都有
→0时,σi(t,h)有不同的变化率,则称X是空间各向异性随机场。与时间各向异性高斯场类似,空间各向异性随机场也有空域算子自相似高斯随机场,定义为:存在一个d×d矩阵D使得对于所有的常数c>0,都有
(1.1.5)式表明当X沿着时间的各个方向有相同的变化率时,在空间上却表现出不同的变化率,即空间的各向异性。对于空间异性随机场的研究结果相对少一些。例如,阶为α=(α1,…,αd)的高斯随机场,Xiao(1995)给出这类高斯随机场像集和图集的Hausdorff和packing维数;Adler(1981)给出了水平集的Hausdorff维数;Mason和Xiao(2002)构造了一类具有平稳增量算子自相似高斯随机场(简称为算子分数布朗运动),并得到了碰撞概率结果,以及像集的Hausdorff维数是由D的特征值正实数部分来确定的;Didier和Pipiras(2011)通过算子分数布朗运动的谱域和时域积分表示考虑了更为一般的框架,并给出了所有算子分数布朗运动的一个特征刻画。
对于空间各向异性随机场的研究,由于所能用的工具相对较少,因此对于该类随机场的研究结果相对应时间各向异性随机场会少一些,要对这类随机场进行研究,就必需借助于新的工具和方法。
(3)对于时间和空间都是各向异性的随机场,研究结果就更少了。Li和Xiao(2011)将(1.1.3)和(1.1.5)式结起来,构造了一类时空各向异性高斯时空模型,即存在一个N×N矩阵E和一个d×d矩阵D使得对于所有的常数c>0,都有
(1.1.6)式表明当X沿着时间的各个方向有不同的变化率时,在空间上也表现出不同的变化率,即时空的各向异性。Li和Xiao(2011)在文中给出了该随机场的定义,并给出了两种构造平稳随机场的具体方法,即移动平均型和可调和平稳随机场。Sönmez(2016,2018)研究了可调和平稳随机场像集和图集在欧氏度量下的Hausdorff维数。该随机场的协方差结构是这三类随机场中最复杂的,因此该类随机场的很多性质还没确定。
需要注意的是,(1.1.3),(1.1.5)和(1.1.6)式给出的各向异性随机场是具有某种自相似的,但是现实中还有许许多多现象不具有自相似性,因此对于此类问题的研究将更具有现实意义。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




