人工快速渗滤系统中CRI反应器模型构建及规律

CRI系统属于典型的固定床生物膜反应器，污水自上而下或自下而上整体呈推流式流态，在每个微小的局部单元则处于完全混合形态。因此，CRI系统可以看作一个由无数个完全混合的反应器通过连续流串联起来的推流式反应器。

在进行CRI系统基质去除动力学模型构建前，首先做出如下假设：

（1）CRI系统是理想的推流式反应器；

（2）生物膜均匀地附着在滤料上且处于动态平衡状态；

（3）污水在CRI系统内各个层面的流速相同，动力学参数一致；

（4）基质去除主要依靠生物膜上的微生物，污水中的可去除基质均处于溶解态，且不含有微生物；

（5）基质在CRI系统内只沿纵向发生浓度梯度变化，只有横向存在混合现象。

图4-2为CRI反应器的简化模型，其中H为滤料层的总高度，Q为污水流量，S0、S分别为进、出水中基质的浓度，A、r分别为滤柱（滤料）高度h处过水断面的面积和半径。在微生物去除污染物的过程中，当基质浓度较高时以零级反应为主，而当基质浓度较低时以一级反应为主[188]。由于生活污水中的基质浓度相对较低，CRI反应器在稳定运行期间滤料上生物膜对基质的去除规律符合一级反应关系：

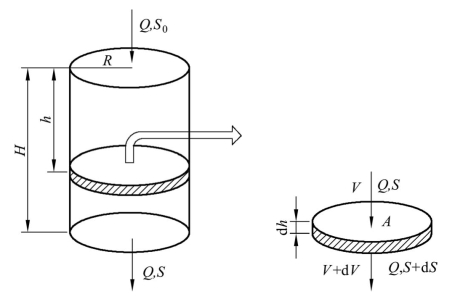
图4-2　CRI反应器简化模型

式中　S——t时间内剩余的基质浓度，mg·L-1；

K——基质去除速率常数，d-1。

根据化学反应动力学和物料守恒原理，单位时间内CRI反应器的每一个局部微元dV都存在着如下物料平衡关系：

式中　W1，W3——CRI反应器局部微元的基质输入量和输出量；

W2——由于生化反应而去除的基质量；

W4——基质在局部微元的变化量（累积量）。

那么CRI系统局部微元dV的NH4+-N平衡关系可写成如下微分方程式：

式中　Q——进水流量，L·d-1；

dS——经过dh高度微元后进出水NH+4-N或NO-2-N的浓度差，mg·L-1；

dV——CRI反应器中微元的容积，L；

dh——CRI反应器中微元的高度，m；

（dS/dt）uA——附着生物膜对NH+4-N或NO-2-N的去除速率，mg·（L·d）-1；

（dS/dt）uS——悬浮微生物对NH+4-N或NO-2-N的去除速率，mg·（L·d）-1；

（dS/dt）——微元dV内NH+4-N或NO-2-N的浓度变化速率，mg·（L·d）-1。

当CRI系统处于稳态运行状态时，单位微元内NH+4-N或NO-2-N浓度变化不大，累积量为零，即NH+4-N或NO-2-N的浓度变化速率（dS/dt）=0，那么：

(www.xing528.com)

于是，式（4-3）可简化为：

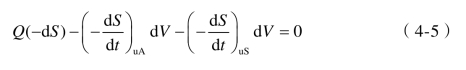
CRI反应器内NH4+-N或NO2--N的去除主要依靠附着生物膜上的微生物，悬浮生长微生物的去除作用可以忽略不计，所以式（4-5）可进一步简化为：

其中，dV=Adh=πr2dh，将式（4-1）代入式（4-6）整理后可得：

令：

式中　m——与CRI滤柱结构、滤料性质、进水流量、基质浓度、生物膜特性、环境条件等相关的NH+4-N或NO-2-N去除速率常数。

将式（4-8）代入式（4-7）可得：

对式（4-9）积分可得：

运算整理后得到：

CRI系统通常采用水力负荷表示进水量，即单位面积CRI系统在单位时间内的处理水量。当CRI系统滤柱结构（包括滤柱材料、形状、半径等）、滤料性质（包括滤料种类、孔隙率、填充方式等）、生物膜特性（包括生物膜厚度、生物膜量、微生物种群等）、环境条件一定时，NH+4-N或NO-2-N去除速率常数m随着进水NH+4-N或NO-2-N浓度（S0，mg·L-1）和水力负荷（q，m·d-1）的变化而变化，那么式（4-8）可表述为：

式中　k——与进水NH+4-N或NO-2-N浓度、水力负荷有关的系数；

α——与进水NH+4-N或NO-2-N浓度有关的系数；

β——与进水水力负荷有关的系数。

将式（4-12）代入式（4-11）可得：

即

式中　h——滤柱（滤料）高度，m；

Sh——滤柱（滤料）高度h处的出水NH+4-N或NO-2-N浓度，mg·L-1；

S0——进水NH+4-N或NO-2-N浓度，mg·L-1；

q——水力负荷，m·d-1。