矩阵的概念及类型，离散数学上册

在许多实际问题中，常会遇到一些数排成的矩形数表。

例如，某工厂生产A、B、C三种产品，每种产品需要甲、乙、丙、丁四种配件数量如表1所示。

表1

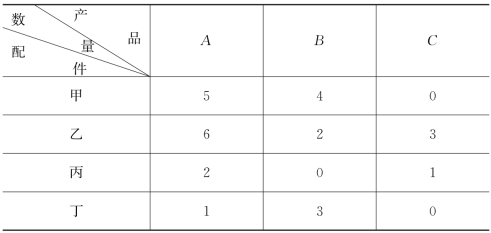
若把表中数字取出且不改变相对位置，就可排成一矩形数表：

又例如，线性方程组：

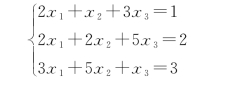
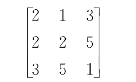
若将其系数取出且不改变相对位置，则可得到一矩形数表

定义1 由m×n个数aij（i=1，2，…，m；j=1，2，…，n）排成m行n列的数表：

称为m行n列矩阵或m×n矩阵。记作

或简记为A=（aij）m×n，其中aij称为矩阵A的第i行第j列元素。元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。

当m=n时，A称为n阶方阵。

只有一行的矩阵

A=(a1 a2 … an)

称为行矩阵或行向量，只有一列的矩阵

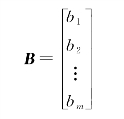
称为列矩阵或列向量。

元素均为零的矩阵称为零矩阵，记作0。(www.xing528.com)

当n阶方阵A=（aij）n×n满足条件：

aij=0(i＞j,i,j=1,2,…,n)

即

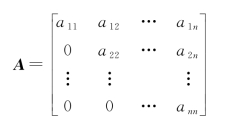
则称矩阵A=（aij）n×n为上三角矩阵，当n阶方阵A=（aij）n×n满足条件：

aij=0(i＜j,i,j=1,2,…,n)

即

则称矩阵A=（aij）n×n为下三角矩阵。

当n阶方阵A=（aij）n×n满足条件：

aij=0(i≠j,i,j=1,2,…,n)

即

则A为n阶对角方阵。特别当aij=1（i=1，2，…，n）时矩阵A称为n阶单位矩阵，记为I，即

若A=（aij）与B=（bij）都是m行n列矩阵，并且满足条件：

aij=bij(i=1,2,…,m;j=1,2,…,n)

则称矩阵A与矩阵B相等，记作A=B。

若矩阵A=（aij）n×n满足条件

aij=aji(i,j=1,2,…,n)

则称矩阵A为n阶对称矩阵。