离散数学上册：推理理论与有效结论

在数学和其他自然科学中，经常考虑从某些前提A1，A2，…，An能够推导出什么结论。例如从分子学说、原子学说能够得到什么结论，从光的波动学说能得到什么结论等。我们一般地要对“假设”的内容作深入分析，并推究其间的关系，从而得到结论。但也有一些推理，只需分析假设中的真值和联结词，便可获得结论。

在实际应用的推理中，我们常常把本门学科的一些定律、定理和条件，作为假设前提，尽管这些前提在数理逻辑中实非永真，但在推理过程中，却总是假设这些命题为T，并使用一些公认的规则，得到另外的命题，形成结论，这种过程就是论证。

定义1 设A和C是两个命题公式，当且仅当A→C为一重言式，即A⇒C，称C是A的有效结论，或C可由A逻辑地推出。

这个定义可以推广到有m个前提的情况。

设H1，H2，…，Hm，C都是命题公式，当且仅当

称C是一组前提H1，H2，…，Hm的有效结论。

判别有效结论的过程就是论证过程，论证方法千变万化，但基本方法是真值表法、直接证法和间接证法。

（1）真值表法

设P1，P2，…，Pn是出现于前提H1，H2，…，Hm和结论C中的全部命题变元，假定对P1，P2，…，Pn作了全部的真值指派，这样就能对应地确定H1，H2，…，Hm和C的所有真值，列出这个真值表，即可看出（1）式是否成立。

因为若从真值表上找出H1，H2，…，Hm真值均为T的行，对于每一个这样的行，若C也有真值T，则（1）式成立，或者看C的真值为F的行，在每一个这样的行中，H1，H2，…，Hm的真值中至少有一个为F，则（1）式也成立。现举例说明如下。

例1 一份统计表格的错误或者是由于材料不可靠，或者是由于计算有错误；这份统计表格的错误不是由于材料不可靠，所以这份统计表格是由于计算有错误。

解 设各命题变元为

P：统计表格的错误是由于材料不可靠。

Q：统计表格的错误是由于计算有错误。

本例可译为：Q是前提P∨Q，」P的有效结论，即

」P∧(P∨Q)⇒Q

我们列出真值表1如下：

表1

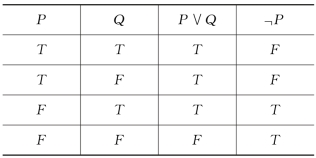
从表上看到，只有在第三行P∨Q和」P的真值都为T，这时Q的真值亦为T。故

(P∨Q)∧(」P)⇒Q

成立。

或者考察Q的真值为F的情况，在第二行和第四行，其相应的P∨Q或」P中至少有一真值为F，故亦说明（P∨Q）∧（」P）⇒Q成立。

例2 如果张老师来了，这个问题可以得到解答，如果李老师来了，这个问题也可以得到解答，总之张老师来了或李老师来了，这个问题就可以得到解答。

解 若设 P：张老师来了。

Q：李老师来了。

R：这个问题可以得到解答。

上述语句可以翻译成下述命题关系式

(P→R)∧(Q→R)∧(P∨Q)⇒R

列出真值表2如下：

表2

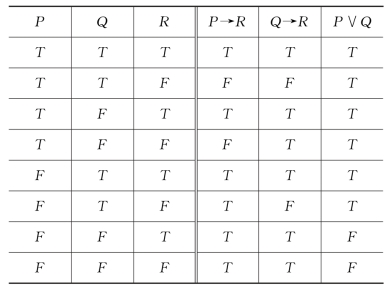
从真值表看到，P→R，Q→R，P∨Q的真值都为T的情况为第一行、第三行和第五行，而在这三行中R的真值均为T。故

(P→R)∧(Q→R)∧(P∨Q)⇒R

（2）直接证法

直接证法就是由一组前提，利用一些公认的推理规则，根据已知的等价或蕴涵公式，推演得到有效的结论。

P规则 前提在推导过程中的任何时候都可以引入使用。(www.xing528.com)

T规则 在推导中，如果有一个或多个公式，等价或蕴涵着公式S，则公式S可以引入推导之中。

在阐述推导过程之前，先列举一些常用的蕴涵式和等价式，为了引用上的方便，将它们加以编号。

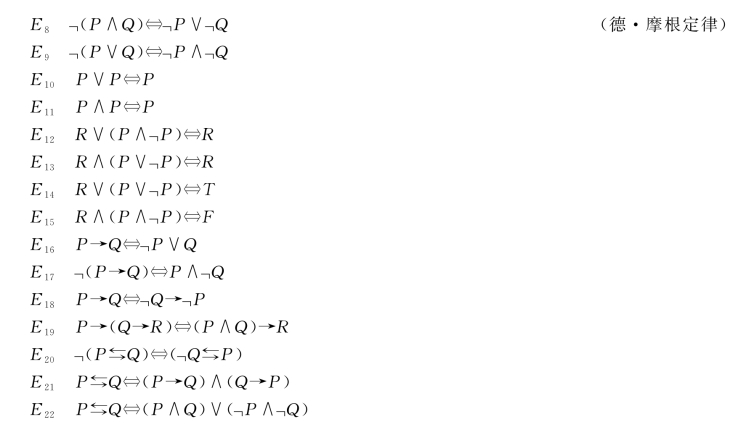
上述各蕴涵式和等价式，并非互相全是独立的，即选取其中少数几个作为基本的，并且遵守规则，就能够推导出其余的来。这里将不进行公理性研究，仅对其中少数几个加以说明。

下面将举例说明这种推导过程。

例3 试证明，R∨S是前提C∨D，（C∨D）→」H，」H→（A∧」B）和（A∧」B）→（R∨S）的有效结论。

第二列上的编号，不仅代表着同一行上的命题公式，而且表明了该公式是处在推导过程中的哪个行上。在右侧，P和T表示所根据的推理规则。继之是注释，它指出了是根据哪些等价式或蕴涵式求得该特定公式的。

例4 证明（W∨R）→V，V→C∨S，S→U，」C∧」U⇒」W。

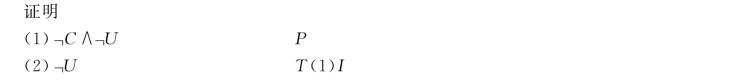
（3）间接证法

定义2 假设公式H1，H2，…，Hm中的命题变元为P1，P2，…，Pn，对于P1，P2，…，Pn的一些真值指派，如果能使H1∧H2∧…∧Hm的真值为T，则称公式H1，H2，…，Hm是相容的。如果对于P1，P2，…，Pn的每一组真值指派使得H1，H2，…，Hm的真值均为F，则称公式H1，H2，…，Hm是不相容的。

现在可把不相容的概念应用于命题公式的证明。

设有一组前提H1，H2，…，Hm，要推出结论C，即证H1∧H2∧…∧Hm⇒C，记作S⇒C，即」C→」S为永真，或C∨」S为永真，故」C∧S为永假。因此要证明H1∧H2∧…∧Hm⇒C，只要证明H1，H2，…，Hm与」C是不相容的。

例5 证明A→B，」（B∨C）可逻辑推出」A。

证明

例6 证明（P∨Q）∧（P→R）∧（Q→S）⇒S∨R。

证明

间接证法的另一种情况是：若要证明H1∧H2∧…∧Hm⇒（R→C），设H1∧H2∧…∧Hm为S，即证S⇒（R→C）或S⇒（」R∨C），故S→（」R∨C）为永真式。因为S→（」R∨C）⇔」S∨（」R∨C）⇔（」S∨」R）∨C⇔」（S∧R）∨C⇔（S∧R）→C，所以若将R作附加前提，如有（S∧R）⇒C，即证得S⇒（R→C）。由（S∧R）⇒C，证明S⇒（R→C）称为CP规则。

例7 证明A→（B→C），」D∨A，B蕴涵D→C。

证明

例8 设有下列情况，结论是否有效？

（1）或者是天晴，或者是下雨。

（2）如果是天晴，我去看电影。

（3）如果我去看电影，我就不看书。

结论：如果我在看书则天在下雨。

故本题即证：」（M⇆Q），M→S，S→」R，推出R→Q。