定义1 给定两个命题公式A和B,设P1,P2,…,Pn为所有出现于A和B中的原子变元,若给P1,P2,…,Pn任一组真值指派,A和B的真值都相同,则称A和B是等价或逻辑相等的,记作A⇔B。
例1 证明」P∨Q⇔P→Q。
证明 列出真值表:
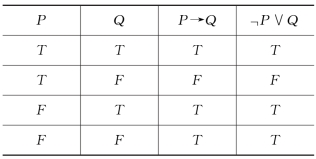
由上表并根据定义可知,」P∨Q⇔P→Q。
例2 证明P⇆Q⇔(P→Q)∧(Q→P)。
证明 列出真值表:
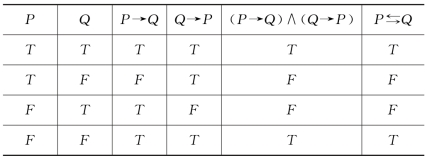
由上表并根据定义知,P⇆Q⇔(P→Q)∧(Q→P)。
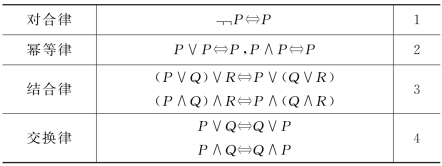
类似地,表1所列出的命题定律,都可以用真值表予以验证。
表1
续表
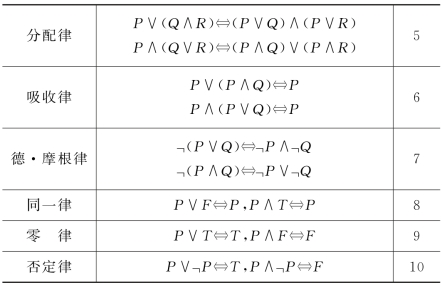
我们已经知道,两个命题公式等价,可以用真值表予以验证。是否还有其他的验证方法呢?我们说还可以用已知的等价式进行推理验证,下面就介绍这种方法。
定义2 如果X是合式公式A的连续的一部分,且X本身也是一个合式公式,则称X为公式A的子公式。
例如,在公式(P→Q)∧(P∨Q)中,(P→Q)就是(P→Q)∧(P∨Q)的子公式。
定理1 设X是合式公式A的子公式,若X⇔Y,将A中的X用Y来置换,所得到的公式B与公式A等价,即A⇔B。
证明 因为在相应变元的任一种指派下,X与Y的真值相同,故以Y取代X后得到公式B,与公式A在相应的指派下,其真值亦相同,故A⇔B。证毕。
例3 证明Q→(P∨(P∧Q))⇔Q→P。
证明 设A:Q→(P∨(P∧Q)),
因为P∨(P∧Q)⇔P,故B:Q→P,即有A⇔B。
例4 证明(P∧Q)∨(P∧」Q)⇔P。
证明(P∧Q)∨(P∧」Q)⇔P∧(Q∨」Q)⇔P∧T⇔P。
例5 证明 P→(Q→R)⇔Q→(P→R)⇔」R→(Q→」P)。
证明 P→(Q→R)⇔」P∨(」Q∨R)⇔」Q∨(」P∨R)⇔Q→(P→R)。
又 P→(Q→R)⇔」P∨(」Q∨R)⇔R∨(」P∨」Q)⇔」R→(Q→」P)。(https://www.xing528.com)
定理2 设A,B为两个命题公式,A⇔B当且仅当A⇆B为一重言式。
证明 若A⇔B,则A,B有相同的真值,即A⇆B永真。反之,若A⇆B为永真,由定义知,A,B真值永远相同,故A⇔B。证毕。
例6 证明」(P∧Q)⇔」P∨」Q。
证明 要证」(P∧Q)⇔」P∨」Q,依据定理2,只需证」(P∧Q)⇆」P∨」Q为永真式,列真值表:
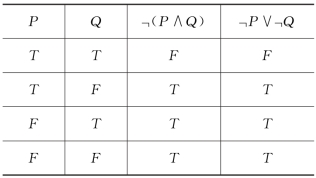
故」(P∧Q)⇔」P∨」Q。
我们知道,联结词⇆可以用→来表达,即A⇆B⇔(A→B)∧(B→A)。
定义3 当且仅当P→Q是一个重言式时,我们称“P蕴涵Q”,并记作P⇒Q。
由定义知,要证明P⇒Q,只需证明P→Q为永真式。而P→Q只有当P为T,Q为F时,P→Q为F,其余各种情况均为T,故只需讨论P为T时Q的取值情况(或Q为F时P的取值情况)。
例7 求证」Q∧(P→Q)⇒」P。
证明 方法1:假设」Q∧(P→Q)为T,则」Q和P→Q均为T,故Q为F,P为F,」P为T,所以」Q∧(P→Q)→」P为T。
方法2:假设」P为F,则P为T。若Q为F,则」Q为T,P→Q为F,所以」Q∧(P→Q)为F,故」Q∧(P→Q)→」P为T。若Q为T,则」Q为F,故」Q∧(P→Q)→」P为T,所以」Q∧(P→Q)⇒」P成立。
表2
表2

所列各蕴涵式都可以如上述推理方法证明。
续表

例8 检验下述论证的有效性:
如果我学习,那么我数学不会不及格,如果我不热衷于玩扑克,那么我将学习。但我数学不及格,因此我热衷于玩扑克。
解 设P:我学习,Q:我数学不及格,R:我热衷于玩扑克。则本题可表示为:
(P→」Q)∧(」R→P)∧Q⇒R
证明上述蕴涵式:假设(P→」Q)∧(」R→P)∧Q为T,则P→」Q,」R→P和Q为T,所以P为F,R为T,因此有(P→」Q)∧(」R→P)∧Q⇒R。本题论述有效。
定理3 设P,Q为任意两个命题公式,P⇔Q的充要条件是P⇒Q且Q⇒P。
证明 必要性:若P⇔Q,则P⇆Q为永真,又因为P⇆Q⇔(P→Q)∧(Q→P),故(P→Q)∧(Q→P)为永真,进而P→Q,Q→P为永真,所以P⇒Q且Q⇒P。
充分性:若P⇒Q且Q⇒P,则P→Q,Q→P为永真,所以(P→Q)∧(Q→P)为永真。因为(P→Q)∧(Q→P)⇔P⇆Q,所以P⇆Q为永真,由定理2知P⇆Q。证毕。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




