在日常语言中,常常使用“或”“与”“但是”等一些联结词,对于这些联结词的使用,一般没有很严格的定义,因此有时显得不太确切。在数理逻辑中,复合命题是由原子命题与逻辑联结词组合而成,联结词是复合命题中的重要组成部分,为了便于书写和进行推演,必须对联结词作出明确规定并符号化。下面就介绍几个能联结命题的联结词及其符号规定。
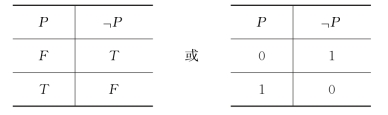
定义1 用“P”表示一个命题,可以把“P”的否定写成“」P”,读作“非P”,“非P”是真当且仅当“P”是假。表1说明了否定的定义。
表1 否定的真值表
现在来说明如何构成命题的否定。为此,考察命题
P:天津是一个城市。
于是」P:天津不是一个城市。
P是真命题,」P是假命题。
再看命题:
P:雪是黑的。」P:雪不是黑的。
命题P是假的,而命题」P是真的。由此知,命题的真假与其否定的真假恰好相反。
另外一个联结词是合取,用符号∧表示。
定义2 给定两个命题P和Q,命题P∧Q读作“P与Q”。命题P∧Q的真值是T当且仅当P和Q的真值全是T。
表2说明了联结词合取的定义。
表2 合取的真值表

例1 试生成下列命题的合取:
P:我们去植树。
Q:房间里有一架电视机。
解 我们去植树与房间里有一架电视机。
例2 将下列命题变换成符号形式的命题:
张明与李华在吃饭。
解 为了写成两个命题的合取,首先把上述命题改写成:
张明在吃饭与李华在吃饭。
再把两个原子命题分别表示成:
P:张明在吃饭。
Q:李华在吃饭。
于是,可把给定命题写成符号形式的命题P∧Q。
在日常语言中,常把合取“与”用于具有某种关系的两个命题之间;但在逻辑学中则不然,完全允许用两个相互无关的原子命题生成新的命题。例如,可以用原子命题“今天下大雨”和“三加三等于六”生成新的命题:
今天下大雨与三加三等于六。
不难看出,所生成的命题是平淡无味的,但在逻辑学中却是允许的。
不难理解,可以把符号∧看成是现代汉语中联结词“与”“和”“并”等词的翻译。然而,在现代汉语中,有时却又在各种不同的意义上使用联结词“与”,因此,不能一概用符号∧去翻译它们。为了说明这种区别,试考察命题:
(1)苹果是红的与香蕉是黄的。
(2)他打开箱子,并拿出一件衣服来。
(3)张小明与张小华是堂兄弟。
命题(1)中的合取“与”和符号∧具有同样的意义。在命题(2)中,“拿出一件衣服来”所描述的行动是发生在“他打开箱子”所描述的行动之后,因此,字词“并”是“于是”的意思,它与合取“与”的意义不同。命题(3)中的字词“与”不是一个合取“与”。就命题P和Q而论,由定义可知合取是对称的。也就是说,给P和Q指派真值,P∧Q和Q∧P的真值相同。因此,如果把命题(1)改写成:
香蕉是黄的与苹果是红的。则不会改变该命题的真值。另一方面,绝不可以把命题(2)改写成:
拿出一件衣服来与他打开箱子。
我们要介绍的第三个联结词是析取,用符号∨表示。
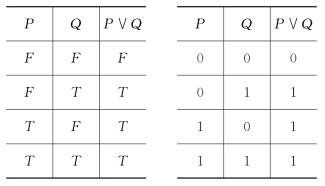
定义3 给定两个命题P和Q,命题P∨Q读作“P或Q”。命题P∨Q的真值是F当且仅当P和Q的真值全是F。
表3说明了析取的定义。
表3 析取的真值表
例3 今天晚上七点我在家看电视,或去剧场看戏。(https://www.xing528.com)
例4 他可能是100米或400米赛跑的冠军。
在例3中的“或”是“排斥或”,例4中的“或”是“可兼或”,而析取指的是“可兼或”,还有一些汉语中的“或”字,实际不是命题联结词。
例5 他昨天做了二十或三十道习题。
例5中的“或”字只是表示了习题的近似数目,不能用联结词“析取”表达,例5是个原子命题。
因此,上述三例中的“或”只有例4可用析取表达。
设P:他是100米赛跑的冠军。
Q:他是400米赛跑的冠军。
P∨Q:他是100米或400米赛跑的冠军。
例6 将命题“今天下雨或者刮风”用符号表示。
解 P:今天下雨。
Q:今天刮风。
P∨Q:今天下雨或者刮风。
要介绍的第4个联结词是条件,用符号→表示。
定义4 给定两个命题P和Q,命题P→Q称为条件命题,读作“如果P,则Q”。这里,当P的真值为T和Q的真值为F时,命题P→Q的真值为F,否则,它的真值为T。
表4说明了条件命题的定义。
表4 条件命题的真值表

例7 设命题P:2×2=4。
Q:(2×2)+1=4+2。
则 P→Q:如果2×2=4,则(2×2)+1=4+2,按规定,P→Q是假命题,这符合直观。
例8 设命题P:2×2=4。
Q:(2×2)+a=4+a。
则 P→Q:如果2×2=4,则(2×2)+a=4+a,按规定,P→Q是真命题,这符合直观。
从上面的例子中可见,关于P→Q的真值规定符合日常生活中语言“如果……,则……”的意思。但是,在对逻辑联结词→的规定中,还有如下情况:如果P是假命题,那么不论Q是真是假,命题“如果P则Q”在逻辑中都被认为是真命题。
例9 设命题P:3×3=8。
Q:教室里有十张桌子。
则 P→Q:如果3×3=8,则教室里有十张桌子,是真命题。
这个命题在日常语言中是毫无意义的,但由于它满足条件命题的定义,因而在逻辑学中却完全可以接受它。
依据定义4,复合命题P→Q的真或假,仅依赖于命题P和Q的真或假,而与它们的含义无关。也就是说,为了组成复合命题P→Q,在前件P和后件Q之间,不要求有任何类型的关系存在,这种条件命题,有时称为实质条件命题。显然,表4所定义的就是个实质条件命题。
在日常语言中,通常只有当两个条件命题之间有某种形式上和内容上的联系时,才可以用联结词“如果……,则……”把它们联结起来,这种条件命题有时称为形式条件命题。一般说来,一个形式条件命题,常常同时又是一个实质条件命题;反之,一个实质条件命题却不一定同时又是一个形式条件命题。我们约定,当不加区别地使用术语“条件命题”时,是指实质条件命题。
在汉语中还有这种情形:能够用一个符号“→”正确地翻译各种不同的表达式。例如,可用命题P→Q表示“假若P,那么Q”;“若P,则Q”;“仅当P,则Q”;“对于Q来说,P是充分的”等。在数学或其他一些数理逻辑著作中,条件命题“如果P,则Q”和“P蕴涵Q”在使用上是等价的,亦即是可互换的,甚至是指同一个关系而言。
最后介绍第五个联结词“双条件”,用符号“⇆”表示。
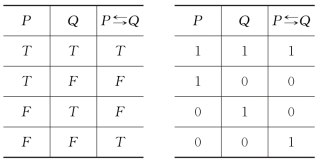
定义5 给定两个命题P和Q,命题P⇆Q称为双条件命题,读作“P当且仅当Q”,当P和Q的真值相同时,P⇆Q的真值为T,否则为假。
表5给出了联结词双条件的定义。
表5 联结词“⇆”的真值表
例10 设命题P:两个三角形全等。
Q:这两个三角形的三个对应边也相等。
则 ![]() :两个三角形全等当且仅当这两个三角形的三组对应边也相等。
:两个三角形全等当且仅当这两个三角形的三组对应边也相等。
例11 设命题P:2+2=4。
Q:雪是白的。
则 P⇆Q:2+2=4当且仅当雪是白的。
与前面的联结词一样,双条件命题也可以不顾其因果联系,而只根据联结词定义确定真值。双条件联结词亦可记作“↔”,或者“iff”。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




