布尔代数是一种特殊的格|格的概念与示例

本章介绍两种重要的代数系统——格与布尔代数。这两种代数系统在计算机科学中有着广泛的应用。布尔代数实际上是一种特殊的格。

虽然格是一种代数系统，但我们可以从部分序集的角度给出格的定义。这种定义与格的代数系统定义是等价的，但是具有直观的哈斯（Hasse）图表示，因而比较容易理解与掌握。

定义1 设（L，≤）是一个半序集。如果对于任意a，b∈L，L的子集{a，b}在L中都有一个最大下界（记作inf{a，b}）和一个最小上界（记作sup{a，b}），则称（L，≤）是一个半序格。

显然，一个序集是一个格。但是，不是所有半序集都是格，这可由下面某些半序集的哈斯图看到。

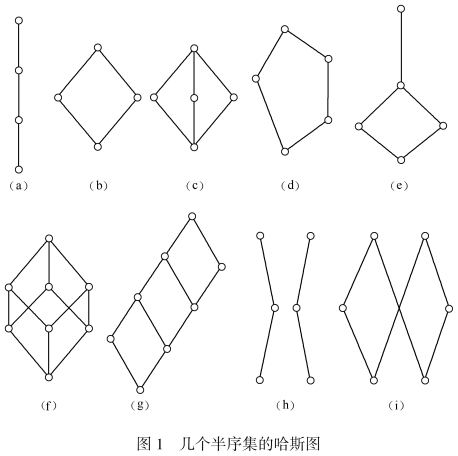
图（a）是序集，也是格；（b）～（g）是半序集，也是格；图（h），（i）是半序集，但不是格。

下面给出一些格的例子，这些例子在本章中经常要用到。

例1 设S是任意集合，ρ（S）是S的幂集合，则（ρ（S），⊆）是一个半序关系。对于ρ（S）中任意元素A，B，{A，B}在ρ（S）中有最大下界inf{A，B}=A∩B，以及最小上界sup{A，B}=A∪B，所以半序集（ρ（S），⊆）是一个格。

当S仅有一个元素时，对应的格是包括两个元素的链。当S有两个元素时，对应的格是图（b）。当S有3个元素时，对应的格是图（f）。

例2 设Z+是所有正整数集合。D是Z+中的“整除关系”，亦即，对任意a，b∈Z+，aDb当且仅当a整除b，则（Z+，D）显然是一个半序关系。

容易说明，Z+中子集{a，b}的最小上界就是a，b的最小公倍数，子集{a，b}的最大下界就是{a，b}的最大公因数，因此（Z+，D）是一个格。

例3 设n是一个正整数，Sn 是n的所有因数的集合。例如

S6={1,2,3,6},S24={1,2,3,4,6,8,12,24}

设D是“整除关系”，于是（S6，D）是格，其哈斯图是图（b）；（S8，D）是格，其哈斯图是图（a）；（S24，D）是格，其哈斯图是图（g）；（S30，D）是格，其哈斯图是图（f）。

下面我们再从代数系统的观点介绍格的概念。

定义2 设L是一个集合，×，⊕是L中两个二元运算。如果这两种运算满足如下算律，则称此代数系统（L，×，⊕）为代数格：

（1）交换律：a×b=b×a，a⊕b=b⊕a；

（2）结合律：a×（b×c）=（a×b）×c，

a⊕(b⊕c)=(a⊕b)⊕c;

（3）吸收律：a×（a⊕b）=a，a⊕（a×b）=a。其中a，b，c是L中任意元素。

例4 设S是一个集合，ρ（S）是S的幂集合，集合的交（∩）、并（∪）是ρ（S）上两个代数运算，满足代数格所要求的3条算律，所以（ρ（S），∩，∪）是一个代数格。

例5 设Z+是所有正整数集合，两个正整数的最大公因数×、最小公倍数⊕可以看成是Z+上两个代数运算。容易证明这两个代数运算满足代数格所要求的3条算律，因此（Z+，×，⊕）是一个代数格。

例6 设n是一个正整数，Sn是n的所有因数的集合，两个正整数的最大公因数×、最小公倍数⊕可以看作是Sn上两个代数运算，于是，（Sn，×，⊕）是一个代数格。

以上我们给出了两种格的定义，一种是半序格，一种是代数格。下面我们证明这两种定义实际上是等价的。

定理1 一个半序格必然是一个代数格；反之亦然。

证明 先证定理的第一部分。

设（L，≤）是半序格，则对任意a，b∈L，记inf{a，b}=a×b；sup{a，b}=a⊕b。由于对任意a，b其inf{a，b}，sup{a，b}是唯一的，所以，如上定义的×，⊕是集合L上的两种二元运算。

我们先证明×，⊕运算满足吸收律。即对任意a，b∈L，有a×（a⊕b）=a，a⊕（a×b）=a。

因为a×（a⊕b）是a与（a⊕b）的最大下界，所以a×（a⊕b）≤a；另一方面由于a≤a，a≤a⊕b，所以a是a与（a⊕b）的下界，故a≤a×（a⊕b）。因此a=a×（a⊕b）。同理可证a⊕（a×b）=a。

类似地，不难证明×，⊕运算满足交换律和结合律，因此，根据定义，（L，×，⊕）是一个代数格。

再证明定理1的后半部分。

设（L，×，⊕）是一个代数格。在集合L上定义关系≤如下：

对任意a，b∈L，

a≤b⇔a×b=a

以下证明≤是一个半序关系。

因为a×a=a×（a⊕（a×a））=a，所以有a≤a。

若有a≤b，b≤a，则应有a×b=a，b×a=b，但由×运算的交换律，a×b=b×a，所以a=b。

若a≤b，b≤c，则有a×b=a，b×c=b，再根据×运算的结合律有

a×c=(a×b)×c=a×(b×c)=a×b=a

根据关系≤的定义知a≤c。

由此证明了关系≤具有自反性、反对称性、传递性，故≤是半序关系。(www.xing528.com)

不难证明：a×b=a⇔a⊕b=b。

若a×b=a，则由吸收律

a⊕b=(a×b)⊕b=b

若a⊕b=b，则

a×b=a×(a⊕b)=a

因此，对任意a，b∈L，

a≤b⇔a⊕b=b

下面证明，对任意{a，b}⊆L，存在inf{a，b}，sup{a，b}，才能结束定理的证明。

由吸收律知

a×(a⊕b)=a

b×(a⊕b)=b

故有a≤（a⊕b），b≤（a⊕b），亦即a⊕b是{a，b}的上界。

若c∈L，且c是{a，b}的上界，亦即a≤c，b≤c，则应有a⊕c=c，b⊕c=c，于是

(a⊕b)⊕c=(a⊕b)⊕(c⊕c)

=(a⊕c)⊕(b⊕c)

=c⊕c=c

故有（a⊕b）≤c。这就说明（a⊕b）是{a，b}的最小上界，即sup{a，b}=（a⊕b）。

同理可证，inf{a，b}=a×b。

综上所述，（L，≤）是一个半序格。证毕。

因为半序格与代数格等价，我们今后就不再区分半序格与代数格，而统一称为格，今后，提到一个格，既可以将其理解为半序格，也可以理解为代数格，其×，⊕分别是在半序关系≤下的最大下界运算与最小上界运算。

定义3 设（L，×，⊕）是一个格，S是L的一个子集。如果在×，⊕之下，S是封闭的，则（S，×，⊕）称为（L，×，⊕）的子格。

因为在L中，×，⊕运算满足交换律、结合律和吸收律。若×，⊕在S中运算封闭，而S是L的子集，所以×，⊕运算自然在S中满足交换律、结合律和吸收律，所以（S，×，⊕）是格。

例如，（Sn，×，⊕）是（I+，×，⊕）的子格，其中×，⊕分别是最大公因数和最小公倍数。

最后指出一点：设（L，≤）是一个格，与其等价的代数格为（L，×，⊕），S是L的一个子集。若（S，≤）是一个半序格，则（S，×，⊕）不一定是（L，×，⊕）的子格，因为S在×，⊕运算下未必封闭。

例7 设（L，≤）是一个格，其哈斯图由图2所示。其中L={a1，a2，a3，a4，a5，a6，a7，a8}。

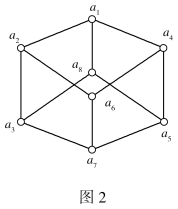
取S1={a1，a2，a4，a6}，则（S1，×，⊕）是（L，×，⊕）的子格。

取S2={a1，a2，a4，a8}，则（S2，×，⊕）不是（L，×，⊕）的子格。因为a2×a4=a6，而a6不在S2中，S2在×运算下不封闭。

例8 设（L，×，⊕）是一个格，a是L的一个元素，S是L的一个子集

S={x|a≤x,x∈L}

证明（S，×，⊕）是（L，×，⊕）的一个子格。

证明 设x1，x2是S中任意两个元素，则因（x1⊕x2）是x1，x2的最小上界，x1≤（x1⊕x2），再由≤关系的传递性知a≤（x1⊕x2），即（x1⊕x2）∈S。

又因为a≤x1，a≤x2，所以a是x1，x2的一个下界，而（x1×x2）是x1，x2的最大下界，所以a≤（x1×x2），即（x1×x2）≤S。

既然S在×，⊕两种运算下都封闭，故S为子格。证毕。

格的一个重要特点是其具有对偶性。设（L，R）是一个格，R是L中的半序关系，则显然R-1也是L中的一个半序关系，于是（L，R-1）也是格。把表示格（L，R）的哈斯图翻转过来，就得到（L，R-1）的哈斯图。（L，R）中的求最大下界与最小上界运算分别对应于（L，R-1）中求最小上界运算与求最大下界运算。因此，格中的一切算律与性质都具有对偶性。

如果格（L，R）中有最大与最小元素，则分别用1和0表示最大、最小元素。由1，0和可代表格中任意元素的变量通过×，⊕运算连接起来的式子叫格中的表达式。例如（a×b）⊕c就是格中表达式。把一个表达式E的⊕换成×，×换成⊕，0换成1（当E中有0时），1换成0（当E中有1时），所得表达式称为E的对偶表达式，记作E*。例如设E=（a×b）⊕c，则E*=（a⊕b）×c。根据格的对偶性可以证明如下两个对偶原理。

（1）若XRY在格（L，R）中成立，则Y*RX*也在（L，R）中成立。其中X*，Y*分别是X，Y的对偶表达式。

例如，由（a×b）⊕c≤a⊕c，运用对偶原理1可得a×c≤（a⊕b）×c。

（2）在格（L，R）中，若在条件HRG下，有XRT，则在对偶条件H*R-1G*下，有X*R-1T*。

例如，当b≤c时，有a×b≤a×c；c≤b时，有a⊕c≤a⊕b。