同态与同构：离散数学（上册）中的研究成果

这一节，我们讨论两个代数系统之间的联系。着重研究两个代数系统之间的同态关系和同构关系。

定义1 设＜A；☆＞，＜B；*＞是两个代数系统，☆和*分别是A和B上的二元（n元）运算，设f是从A到B的一个映射，使得对任意的a1，a2∈A，有

f(a1☆a2)=f(a1)*f(a2)

则称f为由＜A；☆＞到＜B；*＞的一个同态映射，称＜A；☆＞同态于＜B；*＞，记作A～B。把＜f（A）；*＞称为＜A；☆＞的一个同态象，其中

f(A)={x|x=f(a),a∈A}⊆B

两个代数系统在同态意义下的相互联系可以由图1来描述。

例1 考察代数系统＜Z；·＞，这里Z是整数集，·是普通乘法运算。如果我们只对运算结果中正、负、零之间的特征区别感兴趣，那么，代数系统＜Z；·＞中运算结果的特征就可以用另一个代数系统＜B；☉＞的运算结果来描述，其中B={正，负，零}，☉是定义在B上的二元运算，如表1所示。

作映射f：I→B如下：

表1

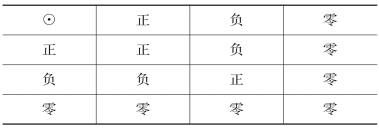
很明显，对于任意的a，b∈Z有

f(a·b)=f(a)☉f(b)

因此，映射f是由＜Z；·＞到＜B；☉＞的一个同态。

例1告诉我们，在＜Z；·＞中研究运算结果的正、负、零的特征就等于在＜B；☉＞中的运算特征，可以说，代数系统＜B；☉＞描述了＜Z；·＞中运算结果的基本特征。而这正是研究两个代数系统之间是否存在同态的重要意义。

应该指出，由一个代数系统到另一个代数系统可能存在着多于一个的同态。

例2 设＜Z；+＞是整数加法群，＜I5，+5＞是在模5的加法下的加法群，其中I5={[0]，[1]，[2]，[3]，[4]}，模5加法运算+5定义为：。f是从＜Z；+＞到＜I5；+5＞的一个映射，定义为：对任意。例如f（0）=[0]，f（3）=[3]；f（6）=[1]，f（9）=[4]等，则对任意a，b∈Z，

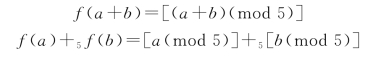
根据数论中模运算的性质，我们知道

即

f(a+b)=f(a)+5f(b)

所以f是＜Z；+＞到＜I5；+5＞的同态映射。

定义2 设f是由＜A；☆＞到＜B；*＞的一个同态，如果f是从A到B的一个满射，则f称为满同态；如果f是从A到B的一个入射，则称f为单一同态；如果f是从A到B的一个双射，则称f为同构映射，并称＜A；☆＞和＜B；*＞是同构的，记作A≌B。

例3 设f：R→R对任意x∈R，

f(x)=5x

那么，f是＜R；+＞到＜R；·＞的一个单一同态。

例4 设f：N→Nk定义为对任意的x∈N，

那么，f是从＜N；+＞到＜Nk；+k＞的一个满同态。

例5 设H={x|x=dn，d是某一个正整数，n∈Z}，定义映射，f：Z→H为对任意n∈Z

f(n)=dn

那么，f是＜Z；+＞到＜H；+＞的一个同构，所以Z≌H。

例6 设A={a，b，c，d}，在A上定义一个二元运算如表2所示。又设B={α，β，γ，δ}，在B上定义一个二元运算如表3所示。证明＜A；☆＞和＜B；*＞是同构的。

表2

证明 考察映射f，使得

f(a)=α,f(b)=β,f(c)=γ,f(d)=δ

显然，f是一个从A到B的双射，由表2和表3容易验证f是由＜A；☆＞到＜B；*＞的一个同态。因此，＜A；☆＞和＜B；*＞是同构的。

表3

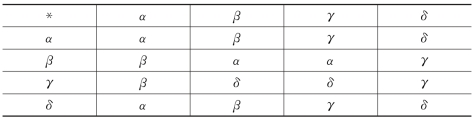
如果考察映射g，使得

g(a)=δ,g(b)=γ,g(c)=β,g(d)=α

那么，g也是由＜A；☆＞到＜B；*＞的一个同构。

例6告诉我们，当两个代数系统是同构的话，它们之间的同构映射可以是不唯一的。

例7 表4中的代数系统＜B；⊕＞和＜C；*＞都是与代数系统＜A；☆＞同构的。

表4

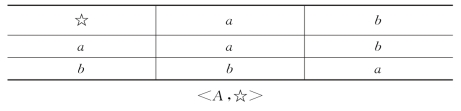
续表

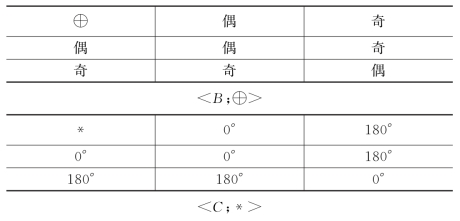
同构这个概念很重要。从上例中可以看到，形式上不同的代数系统，如果它们是同构的话，那么，就可想象地把它们看作是本质上相同的代数系统，所以不同的只是所用的符号不同。并且，容易看出同构的逆仍是一个同构。

定义3 设＜A；☆＞是一个代数系统，如果f是由＜A；☆＞到＜A；☆＞的同态，则称f为自同态。如果g是由＜A；☆＞到＜A；☆＞的同构，则称g为自同构。

定理1 设G是代数系统的集合，则G中代数系统之间的同构关系是等价关系。

证明 因为任何一个代数系统＜A；☆＞可以通过恒等映射与它自身同构，即自反性成立。关于对称性，设＜A；☆＞≌＜B；*＞且有对应的同构映射f，因为f的逆是由＜B；*＞到＜A；☆＞的同构映射，即＜B；*＞≌＜A；☆＞。最后，如果f是由＜A；☆＞到＜B；*＞的同构映射，g是由＜B；*＞到＜C；Δ＞的同构映射，那么g·f就是＜A；☆＞到＜C；Δ＞的同构映射。因此，同构关系是等价关系。

定理2 设f是从代数系统＜A；☆＞到代数系统＜B；*＞的同态映射。

（1）如果＜A；☆＞是半群，那么在f作用下，同态象＜f（A）；*＞也是半群。

（2）如果＜A；☆＞是独异点，那么在f作用下，同态象＜f（A）；*＞也是独异点。

（3）如果＜A；☆＞是群，那么在f作用下，同态象＜f（A）；*＞也是群。

证明（1）设＜A；☆＞是半群且＜B；*＞是一个代数系统，如果f是由＜A；☆＞到＜B；*＞的一个同态映射，则f（A）⊆B。

对于任意的a，b∈f（A），必有x，y∈A使得

f(x)=a,f(y)=b

在A中，必有Z=x☆y，所以

a*b=f(x)*f(y)=f(x☆y)=f(Z)∈f(A)

最后，*在f（A）上是可结合的，这是因为：对于任意的a，b，c∈f（A），必有x，y，z∈A，使得(www.xing528.com)

f(x)=a,f(y)=b,f(z)=c

因为☆在A上是可结合的，所以

a*(b*c)=f(x)*(f(y)*f(z))=f(x)*f(y☆z)

f(x☆(y☆z))=f((x☆y)☆z)=f(x☆y)*f(z)=(f(x)*f(y))*f(z)=(a*b)*c

因此，＜f（A）；*＞是半群。

（2）设＜A；☆＞是独异点，e是A中的幺元，那么f（e）是f（A）中的幺元。这是因为对于任意的a∈f（A）必有x∈A使f（x）=a，所以

a*f(e)=f(x)*f(e)=f(x☆e)=f(x)=a=f(e☆x)=f(e)*f(x)=f(e)*a

因此，＜f（A）；*＞是独异点。

（3）设＜A；☆＞是群。

对于任意的a∈f（A）必有x∈A使f（x）=a。因为＜A；☆＞是群，故x有逆元x-1，且f（x-1）∈f（A），而

f(x)*f(x-1)=f(x☆x-1)=f(e)=f(x-1☆x)

=f(x-1)*f(x)

所以，f（x-1）是f（x）是逆元。即

f(x-1)=f(x)-1

因此，＜f（A）；*＞是群。

定义4 设f是由群＜G；☆＞到群＜G′；*＞的同态映射，e′是G′中的幺元，设Ker（f）={x|x∈G，且f（x）=e′}，称Ker（f）是同态映射f的核，简称f的同态核。

定理3 设f是由群＜G；☆＞到＜G′；*＞的同态映射，则f的同态核K是G的子群。

证明 由定理2可知，e′=f（e）。设k1，k2∈K，则

f(k1☆k2)=f(k1)*f(k2)=e′*e′=e′

故k1☆k2∈K。

对任意的k∈K，由定理2可知

f(k-1)=f(k)-1=e′-1=e′

故k-1∈K。因此，＜K；☆＞是＜G；☆＞的子群。

下面，我们进一步讨论同态与同余关系的对应。为此先介绍同余关系的概念。

定义5 设＜A；☆＞是一个代数系统，并设R是A上的一个等价关系。如果当＜a1，a2＞＜b1，b2＞∈R时，蕴涵着＜a1☆b1，a2☆b2＞∈R，则称R为A上关于☆的同余关系。由这个同余关系将A划分成的等价类称为同余类。

例8 设A={a，b，c，d}，对于由表5所确定的代数系统＜A；☆＞以及由表6所定义的在A上的等价关系R，容易验证，R是A上的同余关系。这个同余关系将A划分成同余类为{a，b}和{c，d}。

表5

例9 设A={a，b，c，d}对于表7所定义的代数系统＜A；☆＞以及由表6所定义的在A上的等价关系R。

表6

表7

由于对＜a，b＞，＜c，d＞∈R有

＜a☆c,b☆d＞=＜d,a＞∉R

因此，由表6所定义的在A上的等价关系R不是一个同余关系。

由上述两例可知：在A上定义的等价关系R，不一定是A上的同余关系，这是因为同余关系必须与定义在A上的二元运算密切相关。

定理4 设＜A；☆＞是一个代数系统，R是A上的一个同余关系，B={A1，A2，…，Ar}是R在A上的等价类集合，那么，必定存在新的代数系统＜B；*＞，它是＜A；☆＞的同态象。

证明 在B上定义二元运算*为：对于任意的Ai，Aj∈B，任取a1∈Ai，a2∈Aj，如果a1☆a2∈Ak，则Ai*Aj=Ak。由于R是A上的同余关系，所以，以上定义的Ai*Aj=Ak是唯一的。

作映射

f(a)=Ai,a∈Ai

显然，f是从A到B的满映射。

对于任意的x，y∈A，x，y必属于B中的某两个等价类，不妨设x☆y∈Ak，于是，就有

f(x☆y)=Ak=Ai*Aj=f(x)*f(y)

因此，f是由＜A；☆＞到＜B；*＞的满同态，即＜B；*＞是＜A；☆＞的同态象。

定理5 设f是由＜A；☆＞到＜B；*＞的一个同态映射，如果在A上定义二元关系R为：＜a，b＞∈R，当且仅当

f(a)=f(b)

那么，R是A上的一个同余关系。

证明 因为f（a）=f（b），所以＜a，a＞∈R。若＜a，b＞∈R，则f（a）=f（b），即f（b）=f（a），所以＜b，a＞∈R。若＜a，b＞∈R，＜b，c＞∈R，则f（a）=f（b）=f（c），所以＜a，c＞∈R。最后，又因为若＜a，b＞∈R，＜c，d＞∈R，则有

f(a☆c)=f(a)*f(c)=f(b)*f(d)=f(b☆d)

所以，＜a☆c，b☆d＞∈R。

因此，R是A上的同余关系。

形象地说，一个代数系统的同态象可以看作是当抽去该系统中某些元素的次要特征的情况下，对该系统的一种粗糙描述。如果我们把属于同一个同余类的元素看作是没有区别的，那么原系统的性态可以用同余类之间的相互关系来描述。现在，用一个例子来说明这一点。

例10 如表8所确定的两个代数系统，＜A；☆＞和＜B；*＞。

表8

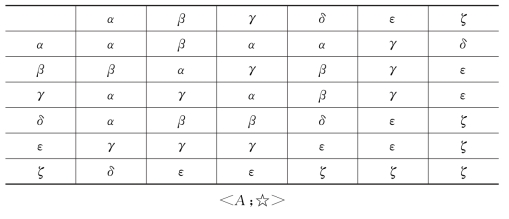
续表

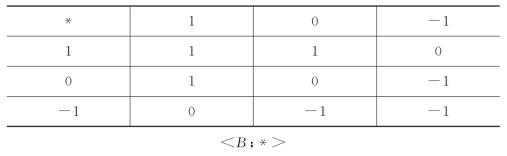
映射

f(α)=1 f(β)=1 f(γ)=1

f(δ)=0 f(ε)=0 f(ζ)=-1

明显地是由代数系统＜A；☆＞到＜B；*＞的一个同态映射。假如把代数系统＜A；☆＞看作是对六个带电粒子α，β，γ，δ，ε，ζ相互作用的详尽描述，如果α，β，γ是带正电荷的粒子；δ，ε是中性粒子；ζ是带负电荷的粒子，那么，我们就可用1，0，-1分别表示这三类粒子，这就是映射f所具有的特性。若记

B={1,0,-1}

那么，代数系统＜B；*＞描述了这三类粒子的相互作用，它正好是代数系统＜A；☆＞的粗糙描述。